Data Science III-B: Estadística descriptiva bidimensional. Una variable cualitativa y otra cuantitativa

Felipe Maggi.

Lenguaje de programación: Python.

En este artículo revisaremos el caso de una variable cualitativa o otra cuantitativa y su representación gráfica más común: los gráficos de caja y bigote, o boxplots. También estudiaremos los gráficos de crestas (o ridgeline plots), como forma alternativa o, más bien, complementaria, de análisis visual.

En esta serie de artículos dedicados a la Ciencia de Datos, ya hemos publicado los capítulos:

Data Science I: Población, muestra, experimentos y tipos de variables.
Data Science II-A: Estadística descriptiva unidimensional. Tablas de frecuencia y gráficos de distribución.
Data Science II-B: Estadística descriptiva unidimensional. Medidas de tendencia central.
Data Science II-C: Estadística descriptiva unidimensional. Medidas de dispersión.
Data Science II-D: Estadística descriptiva unidimensional. Medidas de posición.
Data Science II-E: Estadística descriptiva unidimensional. La curva nornal
Data Science III-A: Estadística descriptiva bidimensional. Dos variables cualitativas

Para cada uno de estos temas hay mucha bibliografía disponible, y nos hemos guiado, en parte, por lo expuesto en el material del Máster de Big Data & Data Science de la Universidad de Barcelona, por Dolores Lorente.

Los conceptos estadísticos son de dominio general, pero cuando tengamos que recurrir a una forma concreta de plantear las cosas, haremos uso, mayoritariamente, de las definiciones expuestas en el libro Estadística general: lo esencial, de Johnson & Kuby.

Conjunto de datos

Antes de continuar, vamos a recuperar el conjunto de datos simulados con los que hemos estado trabajando en toda esta serie de artículos. Recordemos que se trata de las notas de matemáticas obtenidas por alumnos de bachillerato (4 grupos, 40 alumnos por grupo, y 10 temas, lo que hace un total de 1600 notas).

import pandas as pd
import numpy as np
import random
import string
import seaborn as sns
import matplotlib.pyplot as plt

# --- CONFIGURACIÓN INICIAL ---
np.random.seed(42)
random.seed(42)

def generar_id_estudiante(n):
    ids = []
    for _ in range(n):
        id_estudiante = ''.join(random.choices(
            string.ascii_uppercase + string.digits, k=8))
        ids.append(id_estudiante)
    return ids

# --- PARÁMETROS ---
num_estudiantes_por_grupo = 40
total_estudiantes = num_estudiantes_por_grupo * 4
num_notas = 10
ids = generar_id_estudiante(total_estudiantes)
asignatura = 'Matemáticas'
temas = [f'Tema {i+1}' for i in range(num_notas)] # Tema 1 al 10
fecha_inicio = pd.Timestamp('2024-09-01')
grupos = ['A', 'B', 'C', 'D']

# --- FUNCIÓN para generar correlación entre notas y tiempo de estudio ---
def generar_tiempo_estudio(notas, media=270, sd_total=60, correlacion=0.75):
    """
    Genera tiempos de estudio correlacionados con las notas.
    """
    # 1. Calcular desviación estándar de las notas actuales
    sd_notas = np.std(notas)
    if sd_notas == 0: sd_notas = 1 # Evitar división por cero si todas las 
    # notas son iguales
    
    # 2. Calcular la pendiente (m) necesaria
    # Fórmula de regresión: m = r * (Sy / Sx)
    pendiente = correlacion * (sd_total / sd_notas)
    
    # 3. Calcular el ruido residual necesario
    # Para mantener la SD total deseada, el ruido se reduce si la 
    # correlación es alta
    sd_ruido = sd_total * np.sqrt(1 - correlacion**2)
    
    # 4. Generar ruido y calcular tiempo
    ruido = np.random.normal(0, sd_ruido, len(notas))
    tiempo_estudio = media + pendiente * (notas - np.mean(notas)) + ruido
    
    return tiempo_estudio.clip(60, 480).astype(int)

# --- GENERACIÓN DE DATOS ---
data = {
    'id_estudiante': [], 'asignatura': [], 'tema': [], 'fecha': [],
    'nota': [], 'calificacion': [], 'estatura': [], 'sexo': [],
    'tiempo_estudio': [], 'grupo': []
}

# Asignar grupos
grupo_asignado = np.repeat(grupos, num_estudiantes_por_grupo)
random.shuffle(grupo_asignado)

for idx, id_estudiante in enumerate(ids):
    fechas = [fecha_inicio + pd.DateOffset(weeks=i*4) for i in range(num_notas)]
    notas = np.random.normal(6.5, 1, num_notas).clip(0, 10)
    estatura = np.random.uniform(150, 190, num_notas)
    sexo = random.choice(['H', 'M'])

    # Usamos la nueva función (he puesto correlación 0.75 para que 
    # sea bien visible)
    tiempo_estudio = generar_tiempo_estudio(notas, correlacion=0.75)

    for i in range(num_notas):
        data['id_estudiante'].append(id_estudiante)
        data['asignatura'].append(asignatura)
        data['tema'].append(temas[i])
        data['fecha'].append(fechas[i])
        data['nota'].append(round(notas[i], 2))

        if 9 <= notas[i] <= 10: calificacion = 'sobresaliente'
        elif 7 <= notas[i] < 9: calificacion = 'notable'
        elif 5 <= notas[i] < 7: calificacion = 'aprobado'
        else: calificacion = 'suspenso'

        data['calificacion'].append(calificacion)
        data['estatura'].append(estatura[i])
        data['sexo'].append(sexo)
        data['tiempo_estudio'].append(tiempo_estudio[i])
        data['grupo'].append(grupo_asignado[idx])

df = pd.DataFrame(data)
df['aprobado'] = df['calificacion'].apply(lambda x: 0 if x == 'suspenso' else 1)

# Asegurar orden correcto de temas
orden_temas = [f'Tema {i}' for i in range(1, 11)]
df['tema'] = pd.Categorical(df['tema'], categories=orden_temas, ordered=True)

# Mostrar el DataFrame
print(df)

     id_estudiante   asignatura     tema      fecha  nota calificacion  \
0         XAJI0Y6D  Matemáticas   Tema 1 2024-09-01  7.00     aprobado   
1         XAJI0Y6D  Matemáticas   Tema 2 2024-09-29  6.36     aprobado   
2         XAJI0Y6D  Matemáticas   Tema 3 2024-10-27  7.15      notable   
3         XAJI0Y6D  Matemáticas   Tema 4 2024-11-24  8.02      notable   
4         XAJI0Y6D  Matemáticas   Tema 5 2024-12-22  6.27     aprobado   
...            ...          ...      ...        ...   ...          ...   
1595      FNKOMV2X  Matemáticas   Tema 6 2025-01-19  4.28     suspenso   
1596      FNKOMV2X  Matemáticas   Tema 7 2025-02-16  7.87      notable   
1597      FNKOMV2X  Matemáticas   Tema 8 2025-03-16  5.41     aprobado   
1598      FNKOMV2X  Matemáticas   Tema 9 2025-04-13  7.76      notable   
1599      FNKOMV2X  Matemáticas  Tema 10 2025-05-11  7.45      notable   

        estatura sexo  tiempo_estudio grupo  aprobado  
0     157.272999    H             357     C         1  
1     157.336180    H             256     C         1  
2     162.169690    H             274     C         1  
3     170.990257    H             185     C         1  
4     167.277801    H             236     C         1  
...          ...  ...             ...   ...       ...  
1595  173.907293    M             252     A         0  
1596  184.787835    M             250     A         1  
1597  185.633286    M             299     A         1  
1598  167.961510    M             189     A         1  
1599  168.372148    M             284     A         1  

[1600 rows x 11 columns]

Datos bivariados

Nuestros autores de referencia definen los datos bivariados como:

«los valores de dos variables diferentes, que se obtienen del mismo elemento poblacional» (Johnson & Kuby).

Los mismos autores explican que «cada una de las dos variables puede ser cualitativa o cuantitativa. En consecuencia, tres combinaciones de tipos de variables pueden formar datos bivariados:

Ambas variables son cualitativas.
Una variable es cualitativa y la otra es cuantitativa (el caso que ahora nos ocupa).
Ambas variables son cuantitativas».

En el artículo anterior de esta serie ya tratamos el caso el que ambas variables son cualitativas, y repasamos las tablas estadísticas de doble entrada, también conocidas como tablas de contingencia.

En este artículo revisaremos el caso de una variable cualitativa o otra cuantitativa y su representación gráfica más común: los gráficos de caja y bigote, o boxplots, que ya vimos en el artículo referente a las medidas de posición, concretamente en el apartado titulado «Resumen de los cinco números».

También revisaremos los gráficos de crestas (o ridgeline plots), como forma alternativa o, más bien, complementaria, de análisis visual.

Según Johnson & Kuby, cuando se tratan datos bivariados, y una de las variables es cualitativa y la otra cuantitativa:

«los valores cuantitativos se ven como muestras separadas, con cada conjunto identificado por los niveles de la variable cualitativa«.

A continuación, vamos a analizar cómo se distribuyen las notas por tema y por grupo. Dejamos como ejercicio de codificación (muy simple) el análisis de la distribición de notas por sexo y calificación.

También como ejercicio se propone a los lectores responder a la siguiente pregunta: ¿existen, en nuestro conjunto de datos, otras combinaciones posibles de variables, siendo una cualitativa y la otra cuantitativa, que tenga sentido analizar?

Temas y notas

Una de las primeras preguntas que un analista podría hacerse es «¿hay alguna diferencia en la distribución de notas según el tema del examen de matemáticas?»

Boxplots

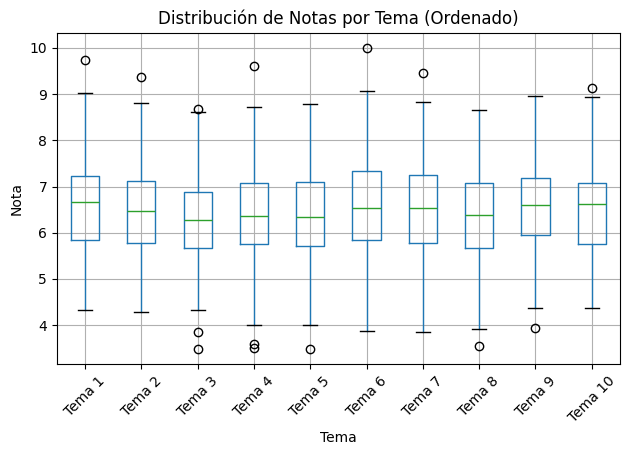
Esto podemos verlo rápidamente con los mencionados gráficos de caja y bigotes. El siguiente código hace precisamente eso: genera boxplots con las notas, agrupadas por temas (hay 160 notas por tema):

import pandas as pd
import matplotlib.pyplot as plt

# 1. Definir el orden correcto de los temas
orden_temas = [f'Tema {i}' for i in range(1, 11)]

# 2. Convertir la columna 'tema' a tipo Categorical con el orden definido
# Esto fuerza a pandas a respetar este orden en los gráficos y ordenamientos
df['tema'] = pd.Categorical(df['tema'], categories=orden_temas, ordered=True)

# 3. Crear el gráfico
plt.figure(figsize=(12, 6))

# Al crear el boxplot, ahora respetará el orden categórico
df.boxplot(column='nota', by='tema', grid=True, rot=45)

# Personalización
plt.title('Distribución de Notas por Tema (Ordenado)')
plt.suptitle('')
plt.xlabel('Tema')
plt.ylabel('Nota')

plt.tight_layout()
plt.show()

Si observamos el gráfico con atención, podemos sacar varias conclusiones:

La distribución de las notas por tema es similar en todos los casos. Las medianas están entre el 6 y el 7, y las cajas y los bigotes son más o menos todos del mismo tamaño, lo que significa que la dispersión es parecida.
El tema 3, sin embargo, parece que fue ligeramente más complicado que los otros. Tanto la mediana como el límite superior son los más bajos. La nota más alta, que es un valor atípico en el conjunto de notas de ese tema, no llega a 9. Es el único tema en el cual el 50% de los datos no se concentra en un intervalo que supere el 7 ($Q3 < 7$).
No hay suspensos en los temas 1, 2 y 10.
Por abajo, tenemos suspensos en los temas 3, 4, 5, 6, 7, 8 y 9, y estudiantes que han obtenido notas atípicamente malas en los temas 3, 4, 5, 8 y 9.
Por arriba, hay estudiantes que han destacado (con notas atípicamente altas) en los temas 1, 2, 3, 4, 6, 7 y 10.
Si hubiera que señalar el tema más sencillo, la elección estaría entre el tema 1 y el 10. Ninguno presenta suspensos, ambos tienen una mediana similar, los dos presentan notas atípicamente altas… Pero, viendo las cajas, y sin hacer cálculos, se podría apostar a que la media del tema 1 es mayor que la del tema 10, aún quitando a los outliers. Más adelante lo comprobaremos.

Gráficos de crestas o cordilleras

Ya sabemos que otra forma de analizar la distribución de una variable numérica o cuantitativa son los gráficos de densidad (tratados con detalle en artículo Data Science II-E: Estadística descriptiva unidimensional. La curva normal).

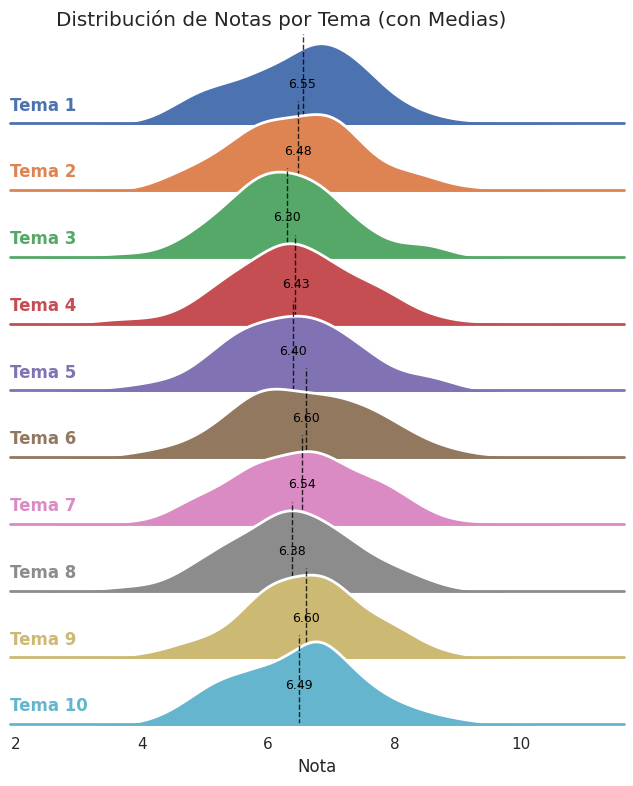
Los gráficos de cresta (ridgeline plot) apilan verticalmente los gráficos de densidad (también se pueden usar histogramas) de cada grupo, lo que permite comparar fácilmente sus distribuciones. El siguiente código genera un ridgeline plot que muestra dichas distribuciones, así como las medias de cada una:

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np # Importamos numpy para calcular la media fácilmente

# Configuración de estilo
sns.set_theme(style="white", rc={"axes.facecolor": (0, 0, 0, 0)})

# Crear el FacetGrid
g = sns.FacetGrid(df, row="tema", hue="tema", aspect=9, height=0.8)

# 1. Dibujar las curvas de densidad
g.map(sns.kdeplot, "nota",
      clip_on=False,
      fill=True,
      alpha=1,
      linewidth=1.5)

# 2. Dibujar el borde blanco
g.map(sns.kdeplot, "nota", clip_on=False, color="w", lw=2)

# --- NUEVO: Función para dibujar la línea de la media ---
def draw_mean_line(x, **kwargs):
    # Calcular la media de los datos del grupo actual
    mean = x.mean()
    # Dibujar la línea vertical
    plt.axvline(mean, color='black', linestyle='--', linewidth=1, alpha=0.8)
    # Opcional: Escribir el valor numérico arriba de la línea
    ax = plt.gca()
    ax.text(mean, 0.4, f'{mean:.2f}', color='black', fontsize=9,
            ha='center', fontweight='light', transform=ax.get_xaxis_transform())

# Mapear la función de la media al gráfico
g.map(draw_mean_line, "nota")
# -------------------------------------------------------

# 3. Dibujar la línea base horizontal
g.map(plt.axhline, y=0, lw=2, clip_on=False)

# 4. Etiquetas de los temas
def label(x, color, label):
    ax = plt.gca()
    ax.text(0, .2, label, fontweight="bold", color=color,
            ha="left", va="center", transform=ax.transAxes)

g.map(label, "nota")

# Ajustes finales de diseño
g.fig.subplots_adjust(hspace=-0.25)
g.set_titles("")
g.set(yticks=[], ylabel="")
g.despine(bottom=True, left=True)

plt.suptitle('Distribución de Notas por Tema (con Medias)', y=0.98)
plt.xlabel('Nota')

plt.show()

Como puede observarse, aunque las distribuciones tienen formas distintas, todas son aproximadamente normales y tienen medias similares. Un analista con cierta experiencia habría concluido lo mismo observando sólo los boxplots (un boxplot es como visualizar un gráfico de densidad desde arriba o en picado).

Aquí también se observa, como se había adelantado antes, que la media del tema 1 es ligeramente superior a la del tema 10.

El tema 3, por su parte, tiene la media más baja de todas, lo que refuerza la hipótesis de que fue el tema más complicado de todos. Sin embargo, ¿es posible afirmar que la media del tema 3 es «significativamente» más baja que la del resto de temas, o que la media general? Los conceptos de hipótesis y significancia estadística no los hemos visto aún, pero los trataremos ampliamente en un artículo dedicado exclusivamente a ellos.

Grupos y notas

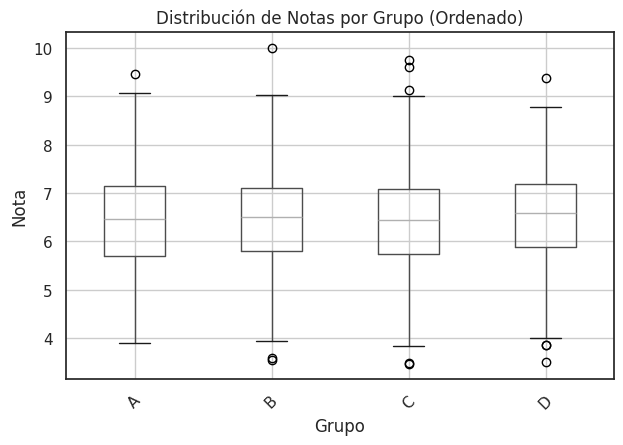
Otra pregunta que podemos hacernos, y muy pertinenente, es si existe alguna diferencia en la distribución de notas entre grupos. Recordemos que hay cuatro grupos de segundo de bachillerato (A, B, C y D). De nuevo, recurriremos a los gráficos de boxplot:

import pandas as pd
import matplotlib.pyplot as plt

# 3. Crear el gráfico
plt.figure(figsize=(12, 6))

# Al crear el boxplot, ahora respetará el orden categórico
df.boxplot(column='nota', by='grupo', grid=True, rot=45)

# Personalización
plt.title('Distribución de Notas por Grupo (Ordenado)')
plt.suptitle('')
plt.xlabel('Tema')
plt.ylabel('Nota')

plt.tight_layout()
plt.show()

Los boxplots presentan pocas diferencias destacables, lo que indica que la distribución de notas es similar en todos los grupos. Ninguno destaca sobre otro.

Por mencionar algunas cosas, podemos decir que el único 10 los obtuvo un alumno del grupo B y que, aunque hay suspensos en todos los grupos, en el A no hay notas atípicamente bajas.

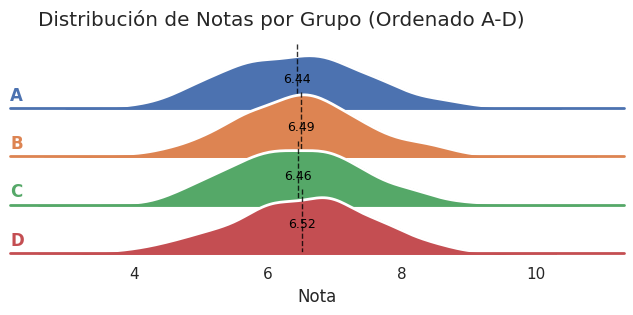
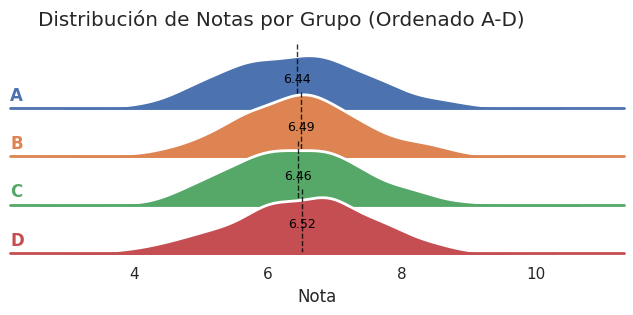
Un ridgeline plot nos va a decir lo mismo en términos generales. A saber, que no hay diferencias sustanciales en las distribuciones de notas por grupo:

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np 

# Configuración de estilo
sns.set_theme(style="white", rc={"axes.facecolor": (0, 0, 0, 0)})

# Crear el FacetGrid
g = sns.FacetGrid(df, row="grupo", hue="grupo", aspect=9, height=0.8)

# 1. Dibujar las curvas de densidad
g.map(sns.kdeplot, "nota",
      clip_on=False,
      fill=True,
      alpha=1,
      linewidth=1.5)

# 2. Dibujar el borde blanco
g.map(sns.kdeplot, "nota", clip_on=False, color="w", lw=2)

# --- NUEVO: Función para dibujar la línea de la media ---
def draw_mean_line(x, **kwargs):
    mean = x.mean()
    plt.axvline(mean, color='black', linestyle='--', linewidth=1, alpha=0.8)
    ax = plt.gca()
    ax.text(mean, 0.4, f'{mean:.2f}', color='black', fontsize=9,
            ha='center', fontweight='light', transform=ax.get_xaxis_transform())

# Mapear la función de la media al gráfico
g.map(draw_mean_line, "nota")

# 3. Dibujar la línea base horizontal
g.map(plt.axhline, y=0, lw=2, clip_on=False)

# 4. Etiquetas de los temas
def label(x, color, label):
    ax = plt.gca()
    ax.text(0, .2, label, fontweight="bold", color=color,
            ha="left", va="center", transform=ax.transAxes)

g.map(label, "nota")

# Ajustes finales de diseño
g.fig.subplots_adjust(hspace=-0.25)
g.set_titles("")
g.set(yticks=[], ylabel="")
g.despine(bottom=True, left=True)

plt.suptitle('Distribución de Notas por Grupo (con Medias)', y=0.98)
plt.xlabel('Nota')

plt.show()

Si tuviéramos que estimar la nota que ha sacado un alumno en uno de los exámenes de matemáticas, saber el tema del examen nos serviría más que saber el grupo al que pertenece el alumno. Hay más variabilidad en las distribuciones por tema, que por grupo. Sin embargo, ninguna de las dos variables (tema y grupo), nos ayudaría a hacer una estimación adecuada. Pero nos estamos adelantando. Queda aún bastante camino para llegar al punto en que podamos estimar (o prever) una nota en base a los datos que tenemos.

En el próximo artículo trataremos el caso de dos variables cuantitativas, y empezaremos a recorrer el camino de baldosas amarillas que conduce desde la correlación y la regresión lineal al Machine Learning, y en última instancia, a la IA Generativa.

Pero no olvidemos que, tal y como se menciona desde el segundo artículo de esta serie, y se destaca en los títulos de cada uno de los artículos posteriores, lo que hemos hecho hasta ahora, y seguiremos haciendo en el artículo siguiente, es estadística descriptiva.

Según el contexto y el tipo de objetivo que persiga nuestro trabajo, esta fase también puede llamarse como Análisis Exploratorio de Datos (EDA, por sus siglas en inglés), y es una etapa esencial que todo analista debe completar, para entender los datos que tiene entre manos, antes de adentrarse en la Cuidad Esmeralda de la IA.

Tabulación cruzada

Cuando se trabaja con variables cuantitativas, ya sea con una o dos, también se pueden usar las tablas de doble entrada que vimos en el artículo anterior, aunque para ello hay que hacer algunos ajustes.

Si la variable cuantitativa es discreta, se puede utilizar directamente. Aunque si el rango de la variable es muy amplio, y cada uno de los valores se repite pocas veces, entonces es preferible agruparlos en intervalos. Una vez agrupados los valores, podemos usar como variable cualitativa la descripción del intervalo. Por ejemplo: [100-150). También podemos usar la marca de clase (C_i) que es el valor central del intervalo (125 en el caso del ejemplo). Si la variable cuantitativa es continua, agrupar los valores tal y como hemos explicado es un paso obligatorio para confeccionar la tabla.

Bibliografía y referencias

Johnson, R. & Kuby, P. (2008). Estadística elemental: lo esencial (10a ed.). Cengage Learning Editores S.A.

Artículo siguiente: Dos variables cuantitativas. Correlación lineal —>

Artículo anterior: <— Dos variables cualitativas

Formulario de contacto de la web datarmony.com	Responder a las personas que nos contactan desde el formulario electrónico de la web.
Cookies, píxel y tracking	Identificar problemas. Obtener datos estadísticos de la navegación de los usuarios. Retener las preferencias del usuario durante su permanencia en un sitio web.
Atención a los derechos de las personas	Atender las solicitudes de los ciudadanos en el ejercicio de los derechos que establece el Reglamento General de Protección de Datos.
Gestión de las comunicaciones recibidas por el canal de denuncias	Crear un canal interno de comunicación para permitir entregar información sobre prácticas irregulares para corregirlas y reparar los daños que hayan podido producir. Proteger a los ciudadanos que informen sobre acciones u omisiones que vulneren el ordenamiento jurídico, afecten a intereses financieros o incidan en el mercado interior.