Felipe Maggi

Lenguaje de programación: Python

En esta serie de artículos dedicados a la Ciencia de Datos, ya hemos publicado los capítulos:

Data Science I: Población, muestra, experimentos y tipos de variables.
Data Science II-A: Estadística descriptiva unidimensional. Tablas de frecuencia y gráficos de distribución.

Vamos a tratar ahora, dentro de la estadística descriptiva unidimensional, las medidas de tendencia central. Quien lea esto quizá piense que es un tema superado, muy básico. Sin embargo, a menudo ocurre que lo que parece simple, no lo es tanto. O siéndolo, se da por sabido. Ambos fenómenos cognitivos acaban en lo mismo: gigantes con pies de barro. Si la base no es sólida, lo que se construya después sobre ella se puede derrumbar como un castillo de naipes.

Por poner un ejemplo: cuando queremos desarrollar un modelo de Machine Learning, y nos encontramos con datos faltantes, una de las técnicas básicas es rellenarlos usando las medidas de tendencia central. ¿Cual de ellas es la más adecuada? Responderemos a esa pregunta cundo llegue el momento.

En este artículo, de nuevo nos guiaremos, en cuanto a estructura, por lo expuesto en material de Máster de Big Data y Data Science de la Universidad de Barcelona, cuya autora es Dolores Lorente porque, desde nuestro punto de vista, fasea la materia de forma adecuada.

Las conceptos estadísticos son de dominio general, pero cuando tengamos que recurrir a una forma concreta de plantear las cosas, haremos uso, mayoritariamente, de las definiciones expuestas en el libro Estadística general: lo esencial, de Johnson & Kuby. Según estos autores,

«Las medidas de tendencia central son valores numéricos que localizan, en algún sentido, el centro de un cojunto de datos. Es frecuente que el término promedio se asocie con todas las medidas de tendencia central«.

Las medidas de tendencia central son:

Media (media aritmética)
Mediana
Moda
Rango medio

Para trabajar con ejemplos, vamos a rescatar el conjunto de datos relativos a las notas obtenidas en los exámenes de matemáticas por los estudiantes de segundo de bachillerato del instituto Luis Vives de Valencia, en el año académico 2024-2025, que utilizamos en el primer artículo de esta serie.

IMPORTANTE: No son las notas de verdad, si no un conjunto de datos generados con fines de ejemplo.

import pandas as pd
import numpy as np
import random
import string

# Establecer semillas para la reproducibilidad
np.random.seed(42)
random.seed(42)

# Función para generar id_estudiante alfanuméricos aleatorios
def generar_id_estudiante(n):
    ids = []
    for _ in range(n):
        id_estudiante = ''.join(random.choices(string.ascii_uppercase + string.digits, k=8))
        ids.append(id_estudiante)
    return ids

# Generar datos
num_estudiantes_por_grupo = 40
total_estudiantes = num_estudiantes_por_grupo * 4
num_notas = 10

ids = generar_id_estudiante(total_estudiantes)
asignatura = 'Matemáticas'
temas = [f'Tema {i+1}' for i in range(num_notas)]
fecha_inicio = pd.Timestamp('2024-09-01')

# Función para generar tiempo de estudio con correlación positiva con notas
def generar_tiempo_estudio(notas, media=270, sd=60, correlacion=0.75):
    ruido = np.random.normal(0, sd, len(notas))
    tiempo_estudio = media + correlacion * (notas - np.mean(notas)) + ruido
    return tiempo_estudio.clip(60, 480).astype(int)

# Generar las notas, fechas y otras columnas
data = {
    'id_estudiante': [],
    'asignatura': [],
    'tema': [],
    'fecha': [],
    'nota': [],
    'calificacion': [],
    'estatura': [],
    'sexo': [],
    'tiempo_estudio': [],
    'grupo': []
}

# Grupos disponibles
grupos = ['A', 'B', 'C', 'D']
num_grupos = len(grupos)

# Asignar aleatoriamente los estudiantes a los grupos
grupo_asignado = np.repeat(grupos, num_estudiantes_por_grupo)
random.shuffle(grupo_asignado)

for idx, id_estudiante in enumerate(ids):
    fechas = [fecha_inicio + pd.DateOffset(weeks=i*4) for i in range(num_notas)]
    notas = np.random.normal(6.5, 1, num_notas).clip(0, 10)
    estatura = np.random.uniform(150, 190, num_notas)
    sexo = random.choice(['H', 'M'])

    tiempo_estudio = generar_tiempo_estudio(notas)

    for i in range(num_notas):
        data['id_estudiante'].append(id_estudiante)
        data['asignatura'].append(asignatura)
        data['tema'].append(temas[i])
        data['fecha'].append(fechas[i])
        data['nota'].append(round(notas[i], 2))

        # Asignar calificación basada en la nota
        if 9 <= notas[i] <= 10:
            calificacion = 'sobresaliente'
        elif 7 <= notas[i] < 9:
            calificacion = 'notable'
        elif 5 <= notas[i] < 7:
            calificacion = 'aprobado'
        else:
            calificacion = 'suspenso'

        data['calificacion'].append(calificacion)
        data['estatura'].append(estatura[i])
        data['sexo'].append(sexo)
        data['tiempo_estudio'].append(tiempo_estudio[i])
        data['grupo'].append(grupo_asignado[idx])

# Crear el DataFrame
df = pd.DataFrame(data)

# Añadir la columna "aprobado"
df['aprobado'] = df['calificacion'].apply(lambda x: 0 if x == 'suspenso' else 1)

# Mostrar el DataFrame
print(df)

     id_estudiante   asignatura     tema      fecha  nota calificacion  \
0         XAJI0Y6D  Matemáticas   Tema 1 2024-09-01  7.00     aprobado   
1         XAJI0Y6D  Matemáticas   Tema 2 2024-09-29  6.36     aprobado   
2         XAJI0Y6D  Matemáticas   Tema 3 2024-10-27  7.15      notable   
3         XAJI0Y6D  Matemáticas   Tema 4 2024-11-24  8.02      notable   
4         XAJI0Y6D  Matemáticas   Tema 5 2024-12-22  6.27     aprobado   
...            ...          ...      ...        ...   ...          ...   
1595      FNKOMV2X  Matemáticas   Tema 6 2025-01-19  4.28     suspenso   
1596      FNKOMV2X  Matemáticas   Tema 7 2025-02-16  7.87      notable   
1597      FNKOMV2X  Matemáticas   Tema 8 2025-03-16  5.41     aprobado   
1598      FNKOMV2X  Matemáticas   Tema 9 2025-04-13  7.76      notable   
1599      FNKOMV2X  Matemáticas  Tema 10 2025-05-11  7.45      notable   

        estatura sexo  tiempo_estudio grupo  aprobado  
0     157.272999    H             357     C         1  
1     157.336180    H             256     C         1  
2     162.169690    H             274     C         1  
3     170.990257    H             185     C         1  
4     167.277801    H             236     C         1  
...          ...  ...             ...   ...       ...  
1595  173.907293    M             252     A         0  
1596  184.787835    M             250     A         1  
1597  185.633286    M             299     A         1  
1598  167.961510    M             189     A         1  
1599  168.372148    M             284     A         1  

[1600 rows x 11 columns]

Media aritmética

Todo el mundo sabe lo que es la media aritmética (que solemos llamar no muy acertadamente como promedio):

La media es la suma de todos los valores de la variable ( $x$ ), dividida por el número total de valores.

Antes de expresar esto matemáticamente, debemos diferenciar entre la media poblacional, y la media muestral.

Media poblacional

La media poblacional se representa con la letra $μ$ (mu).

El número total de valores, en este caso, es el tamaño poblacional, que se representa con la letra $N$ mayúscula.

La media poblacional, matemáticamente hablando, es:

$μ = \frac{\sum x}{N}$

Para el conjunto de datos ${2, 3, 4, 5, 6, 7, 7, 8, 9}$ , y suponiendo que pertenecen a la población,

$μ = \frac{2 + 3 + 4 + 5 + 6 + 7 + 7 + 8 + 9}{9} = 5.6$

Según lo explicado en el primer artículo de esta serie, la media poblacional es un parámetro.

No es frecuente conocer los parámetros, por que no es frecuente contar con los datos de toda la población. A menudo contamos con datos de una muestra de la población.

Aprovechando los datos de ejemplo, con las notas obtenidas en los exámenes de matemáticas por los estudiantes de segundo de bachillerato del instituto Luis Vives de Valencia, en el año académico 2024-2025 (la población), vamos obtener la media de esas notas:

# Calcular la media de la columna nota
media_nota = round(df['nota'].mean(), 2)
print(f"La media de la columna 'nota' es: {media_nota}")

La media de la columna 'nota' es: 6.48

Según estos resultados, la media de la población ( $μ$ ) es 6.48.

Media muestral

La media muestral, como su nombre indica, es la media que se obtiene a partir de una muestra de datos.

En este caso, la variable se sigue demoninando $x$ , pero la media muestral se representa por $\bar{x}$ .

Por su parte, número total de datos (el tamaño muestral), se representa con la letra $n$ minúscula.

Por lo tanto, la expresión matemática de la media muestral es:

$\bar{x} = \frac{\sum x}{n}$

Como ya vimos en el primer artículo de esta serie, la media muestral es un estadístico, a partir del cual podemos inferir datos acerca de la población.

Para obtener una media muestral, antes debemos definir un experimento para obtener una muestra de datos (ver artículo correspondiente), y calcular la media de esa muestra.

# Lista de grupos
grupos = df['grupo'].unique()

# Seleccionar al azar 10 alumnos de cada grupo (sin reemplazo)
alumnos_muestra = []
for grupo in grupos:
  alumnos_grupo = df[df['grupo'] == grupo]['id_estudiante'].unique()
  muestra_grupo = random.sample(list(alumnos_grupo), 10)
  alumnos_muestra.extend(muestra_grupo)

# Seleccionar al azar un tema para cada alumno de la muestra (con reemplazo)
temas_muestra = {}
for alumno in alumnos_muestra:
  notas_alumno = df[df['id_estudiante'] == alumno]
  tema_elegido = random.choice(notas_alumno['tema'].unique())
  temas_muestra[alumno] = tema_elegido

# Crear el DataFrame de muestra con los temas seleccionados
dfs_alumnos_temas = []
for alumno, tema in temas_muestra.items():
  df_alumno_tema = df[(df['id_estudiante'] == alumno) & (df['tema'] == tema)]
  dfs_alumnos_temas.append(df_alumno_tema)

df_muestra_1 = pd.concat(dfs_alumnos_temas, ignore_index=True)

# Calcular la nota media de la muestra
nota_media_muestra_1 = df_muestra_1['nota'].mean()

# Mostrar el DataFrame de muestra y la nota media
print("DataFrame de muestra:")
print(df_muestra_1.head())
print()
print(f"Nota media de la muestra: {nota_media_muestra_1:.2f}")

DataFrame de muestra:
  id_estudiante   asignatura    tema      fecha  nota calificacion  \
0      PKYRYBOV  Matemáticas  Tema 9 2025-04-13  7.36      notable   
1      GNZS43C5  Matemáticas  Tema 5 2024-12-22  7.36      notable   
2      1V2ISQP4  Matemáticas  Tema 2 2024-09-29  6.75     aprobado   
3      JUY0BVR6  Matemáticas  Tema 5 2024-12-22  7.45      notable   
4      MZSGIPPS  Matemáticas  Tema 4 2024-11-24  5.97     aprobado   

     estatura sexo  tiempo_estudio grupo  aprobado  
0  186.512032    M             226     C         1  
1  180.612652    M             266     C         1  
2  177.783817    M             316     C         1  
3  158.972742    M             208     C         1  
4  152.611070    H             246     C         1  

Nota media de la muestra: 6.37

La media muestral de las notas, en este caso es de:

print(f"Nota media de la muestra: {nota_media_muestra_1:.2f}")

Nota media de la muestra: 6.37

Si se repite el experimento, la media muestral será, probablemente, distinta.

Mediana

«La mediana es el valor de los datos que ocupa la posición media, cuando los datos están clasificados en orden de acuerdo con sus valores» (Johnson & Kuby).

La mediana muestral se representa mediante $\tilde{x}$ , y divide al conjunto de datos en dos subconjuntos de tamaños iguales.

Para determinar la mediana, Johnson & Kuby proponen el siguiente procedimiento:

Ordene los datos de menor a mayor.
Determine la profundidad de la mediana: $d (\tilde{x}) = \frac{n + 1}{2}$ , donde $n$ es el número de datos.
Determine el valor de la mediana $\tilde{x}$ , contando los datos ordenados hasta la posición $d (\tilde{x})$ . La mediana es el valor que ocupa dicha posición, y será la misma tanto si cuenta de menor a mayor, como de mayor a menor, hasta $d (\tilde{x})$ .

Mediana para $n$ impar

Si el número de datos ( $n$ ) es impar, la mediana ( $\tilde{x}$ ) es el valor que ocupa la posición central. Por ejemplo, en el conjunto de datos ordenados

${2, 3, 4, 5, 6, 7, 7, 8, 9}$

$n = 9$
$d (\tilde{x}) = \frac{9 + 1}{2} = \frac{10}{2} = 5$
El valor que ocupa la 5ª posición es 6. Por lo tanto, $\tilde{x} = 6$

Mediana para $n$ par

Si el número de datos ( $n$ ) es par, la mediana ( $\tilde{x}$ ) es la semisuma de los dos valores que ocupan la posición central. Por ejemplo, en el conjunto de datos ordenados

${3, 4, 5, 6, 7, 7, 8, 9}$

$n = 8$
$d (\tilde{x}) = \frac{8 + 1}{2} = \frac{9}{2} = 4.5$
La mediana está medio camino entre los datos que ocupan las posiciones 4ª y 5ª, que son 6 y 7, respectivamente. Por lo tanto, la mediana es $\tilde{x} = \frac{6 + 7}{2} = \frac{13}{2} = 6.5$

En el caso caso de los datos de ejemplo, con las notas de matemáticas, estamos trabajando con 1600 observaciones.

Podemos ordenar las notas, contar hasta la posición $d (\tilde{x}) = \frac{1600 + 1}{2} = \frac{1601}{2} = 800.5$ , y dividir entre 2 las notas que ocupen las posiciones 800ª y 801ª.

Cálculo de la mediana con una función paso a paso

La función siguiente hace esto, paso a paso, para que se vea claramente qué estamos calculando.

Es importante advertir que, en este caso, estamos calculando la mediana de la población, no de la muestra:

def calcular_mediana_notas(df):
    # Paso 1: Extraer las notas
    print("Paso 1: Extraer las notas")
    notas = df['nota'].tolist()
    # print(f"Notas: {notas}")

    # Paso 2: Ordenar las notas
    print("Paso 2: Ordenar las notas")
    notas_ordenadas = sorted(notas)
    # print(f"Notas ordenadas: {notas_ordenadas}")

    # Paso 3: Calcular el número total de notas
    print("Paso 3: Contar el número total de notas")
    n = len(notas_ordenadas)
    print(f"Número total de notas: {n}")

    # Paso 4: Verificar si el número de notas es par o impar
    print("Paso 4: Verificar si el número de notas es par o impar")
    if n % 2 == 0:
        print("El número de notas es par")
        # Si es par, la mediana es el promedio de las dos notas centrales
        central_izquierda = n // 2 - 1
        central_derecha = n // 2
        print(f"Las dos notas centrales son: {notas_ordenadas[central_izquierda]} y {notas_ordenadas[central_derecha]}")
        mediana = (notas_ordenadas[central_izquierda] + notas_ordenadas[central_derecha]) / 2
    else:
        print("El número de notas es impar")
        # Si es impar, la mediana es la nota central
        central = n // 2
        print(f"La nota central es: {notas_ordenadas[central]}")
        mediana = notas_ordenadas[central]

    # Paso 5: Mostrar la mediana
    print("Paso 5: La mediana de las notas es:", mediana)

    return mediana

# Usar la función con el DataFrame df
mediana_notas = calcular_mediana_notas(df)
print(f"La mediana de las notas es: {mediana_notas}")

Paso 1: Extraer las notas
Paso 2: Ordenar las notas
Paso 3: Contar el número total de notas
Número total de notas: 1600
Paso 4: Verificar si el número de notas es par o impar
El número de notas es par
Las dos notas centrales son: 6.47 y 6.47
Paso 5: La mediana de las notas es: 6.47
La mediana de las notas es: 6.47

Sin embargo, es mucho más eficiente usar alguna de las funciones de Python, tal como hemos hecho antes con la media aritmética.

Esto último lo hemos mostrado para hacer evidente el proceso de cálculo de la mediana, y lo haremos más adelante, para ejemplificar, cuando sea posible, cómo funciona una función «por dentro». Es muy útil entender qué estamos haciendo, y el problema de las librerías es que hacen los cálculos sin que «veamos nada».

Dicho esto, en Python podemos calcular la mediana de varias maneras, usando la función median de numpy, statistics o de pandas . Esta última es la que mostramos a continuación:

Cáculo de la mediana con la función median() de pandas

mediana_nota = df['nota'].median()
mediana_nota

6.47

Moda

«La moda es es valor de $x$ que se presenta con mayor frecuencia» (Johnson & Kuby)

La moda se representa por $M o$ .

Por ejemplo, en el grupo 1, 1, 2, 2, 2, 3, 4, 5, la moda es 2 ( $M o$ = 2).

Si en un grupo de datos todos los valores tienes la misma frecuencia, entonces no hay moda. Por ejemplo: el grupo 1, 1, 1, 3, 3, 3, 5, 5, 5, 6, 6, 6 no tiene moda.
Si en un grupo de datos tenemos varios valores, y algunos de ellos tienen la misma frecuencia, y dicha frecuencia es la máxima, la distribución se conoce como multimodal (tiene varias modas). Por ejemplo: en el grupo 1, 1, 1, 4, 5, 6, 6, 6, 7, 8, 9, 10, 10, 10, hay tres modas: 1, 6 y 10.
Finalmente, si dos puntuaciones adyacentes presentan la frecuencia máxima, la moda es la media aritmética de esas dos puntuaciones. Por ejemplo: 1, 2, 3, 4, 4, 6, 6, 7, 8, 9, 10 -> $M o = 5$ , pues la media entre 4 y 6 es 5.

moda_nota = df['nota'].mode()[0]
moda_nota

6.18

Rango medio

«Es el número que está exactamente a la mitad entre el valor más bajo (L) y el más alto (H)«

Rango Medio = $\frac{L + H}{2}$

A continuación calculamos el rango medio usando las funciones min() y max() de pandas:

rango_medio_nota = (df['nota'].min() + df['nota'].max()) / 2
rango_medio_nota

6.74

Comparativa de medidas de tendencia central y adelanto informal del concepto de distribución normal

Vamos a comparar ahora las medidas de tendencia central.

print(f"La media de las notas es: {media_nota}")
print(f"La mediana de las notas es: {mediana_nota}")
print(f"La moda de las notas es: {moda_nota}")
print(f"El rango medio de las notas es: {rango_medio_nota}")

La media de las notas es: 6.48
La mediana de las notas es: 6.47
La moda de las notas es: 6.18
El rango medio de las notas es: 6.74

Como puede verse, la media, la mediana, la moda y el rango medio son similares. Media y mediana, en particular, son prácticamente iguales. Esto no es casualidad, porque las notas de matemáticas de los alumnos de segundo de bachillerato tienen una distibución normal.

En una distribución normal pefecta, todas las medidas serían iguales. Eso no suele pasar. Lo que sí ocurre es que cuando los datos se distribuyen de forma aproximadamente normal, las medidas de tendencia central son similares.

IMPORTANTE: que las medidas de tendencia central sean similares no garantiza que la distribución sea normal.

Soy consciente de que nos estamos adelantando un poco, porque aún no hemos definido formalmente el concepto de «normalidad» cuando hablamos de una distribución de datos.

En lugar de eso, vamos a visualizar lo que estamos comentando, y ya definiremos formalmente el tipo de distribución de las notas, cuando llegue el momento:

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statistics

# Función para calcular la moda usando pandas
def calcular_moda_pandas(df):
    return df['nota'].mode()[0]

# Función para calcular el rango medio
def calcular_rango_medio(df):
    minimo = df['nota'].min()
    maximo = df['nota'].max()
    return (minimo + maximo) / 2

# Crear la gráfica de densidad de las notas y marcar media, mediana, moda y rango medio
def graficar_densidad(df):
    # Calcular estadísticas
    media = df['nota'].mean()
    mediana = df['nota'].median()
    moda = calcular_moda_pandas(df)
    rango_medio = calcular_rango_medio(df)

    # Crear la gráfica de densidad
    plt.figure(figsize=(10, 6))
    sns.kdeplot(df['nota'], fill=True, color='blue', label='Densidad')

    # Marcar la media
    plt.axvline(media, color='red', linestyle='-', label=f'Media: {media:.2f}')

    # Marcar la mediana
    plt.axvline(mediana, color='green', linestyle='--', label=f'Mediana: {mediana:.2f}')

    # Marcar la moda
    plt.axvline(moda, color='purple', linestyle='--', label=f'Moda: {moda:.2f}')

    # Marcar el rango medio
    plt.axvline(rango_medio, color='orange', linestyle='--', label=f'Rango medio: {rango_medio:.2f}')

    # Etiquetas y título
    plt.title('Densidad de Notas con Media, Mediana, Moda y Rango Medio')
    plt.xlabel('Notas')
    plt.ylabel('Densidad')
    plt.legend()

    # Personalizar los ticks del eje x para mostrar solo los valores 2 a 9
    plt.xticks([2, 3, 4, 5, 6, 7, 8, 9])

    # Mostrar la gráfica
    plt.show()

# Llamada a la función
graficar_densidad(df)

Como ya habíamos visto en el primer artículo de esta serie, las notas tienen una distribución que parece una campana. Los valores se concentran en torno la medidas de tendencia central, y son menos frecuentes (tienen menor densidad) en los extremos.

Esto también podemos verlo mediante un histograma. La diferencia con el gráfico de densidad es que aquí vemos las frecuencias de los intervalos, en lugar de densidades:

# Crear el histograma de las notas y marcar media, mediana, moda y rango medio
def graficar_histograma(df):
    # Calcular estadísticas
    media = df['nota'].mean()
    mediana = df['nota'].median()
    moda = calcular_moda_pandas(df)
    rango_medio = calcular_rango_medio(df)

    # Crear el histograma
    plt.figure(figsize=(10, 6))
    sns.histplot(df['nota'], bins=11, kde=False, color='skyblue', label='Histograma', edgecolor='black')

    # Marcar la media
    plt.axvline(media, color='red', linestyle='--', label=f'Media: {media:.2f}')

    # Marcar la mediana
    plt.axvline(mediana, color='green', linestyle='--', label=f'Mediana: {mediana:.2f}')

    # Marcar la moda
    plt.axvline(moda, color='purple', linestyle='--', label=f'Moda: {moda:.2f}')

    # Marcar el rango medio
    plt.axvline(rango_medio, color='orange', linestyle='--', label=f'Rango medio: {rango_medio:.2f}')

    # Etiquetas y título
    plt.title('Histograma de Notas con Media, Mediana, Moda y Rango Medio')
    plt.xlabel('Notas')
    plt.ylabel('Frecuencia')
    plt.legend()

    # Mostrar la gráfica
    plt.show()

# Llamada a la función
graficar_histograma(df)

Ambas visualizaciones nos permiten comprobar que las medidas de tendencia central están en torno al 6.5, y que las notas tienden a concentrarse alrededor de ese valor.

Más adelante veremos con más detalle estas cuestiones, pero aquí adelantaremos algo importante: cuando los datos se distibuyen con forma de campana, y la campana es simétrica, la media aritmética es una buena medida de tendencia central.

En el caso de las notas, decir que las notas están en torno al 6.5 es totalmente aceptable. Decir que la media artimética está en torno al 6.5 también lo es.

Ahora bien, si los datos no se distribuyen de esa manera, la media aritmética puede no ser la métrica adecuada para resumir dichos datos.

Distribución sesgada y adelanto informal del concepto de valores atípicos

Vamos a poner un ejemplo que suele levantar ampollas, y que a menudo se usa para desacreditar a las estadísticas.

A continuación vamos a simular un conjunto de datos con los salarios anuales de un grupo de personas seleccionadas al azar:

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats  # Importar para calcular la moda

# Simulación de datos de salarios con más frecuencia en los salarios bajos
np.random.seed(42)  # Para hacer la simulación reproducible
salarios = np.random.lognormal(mean=10, sigma=0.5, size=1000)  # Generar salarios con más concentración en valores bajos

# Crear un DataFrame a partir del array de salarios
df_salarios = pd.DataFrame(salarios, columns=['Salarios'])

# Calcular media, mediana y rango medio
media = df_salarios['Salarios'].mean()
mediana = df_salarios['Salarios'].median()
rango_medio = (df_salarios['Salarios'].max() - df_salarios['Salarios'].min()) / 2  # Calcular el rango medio

# Mostrar resultados
print(f'Media: {media:.2f}')
print(f'Mediana: {mediana:.2f}')
print(f'Rango medio: {rango_medio:.2f}')

# Crear el gráfico de densidad
plt.figure(figsize=(10, 6))
sns.kdeplot(df_salarios['Salarios'], color='skyblue', fill=True)

# Títulos y etiquetas
plt.title('Gráfico de Densidad de Salarios con Media, Mediana y Rango Medio', fontsize=16)
plt.xlabel('Salarios (Euros)', fontsize=12)
plt.ylabel('Densidad', fontsize=12)

# Añadir líneas para la media, mediana y rango medio
plt.axvline(media, color='red', linestyle='--', label=f'Media: {media:.2f}')
plt.axvline(mediana, color='green', linestyle='--', label=f'Mediana: {mediana:.2f}')
plt.axvline(rango_medio, color='orange', linestyle='--', label=f'Rango Medio: {rango_medio:.2f}')

# Añadir leyenda
plt.legend()

# Mostrar la gráfica
plt.show()

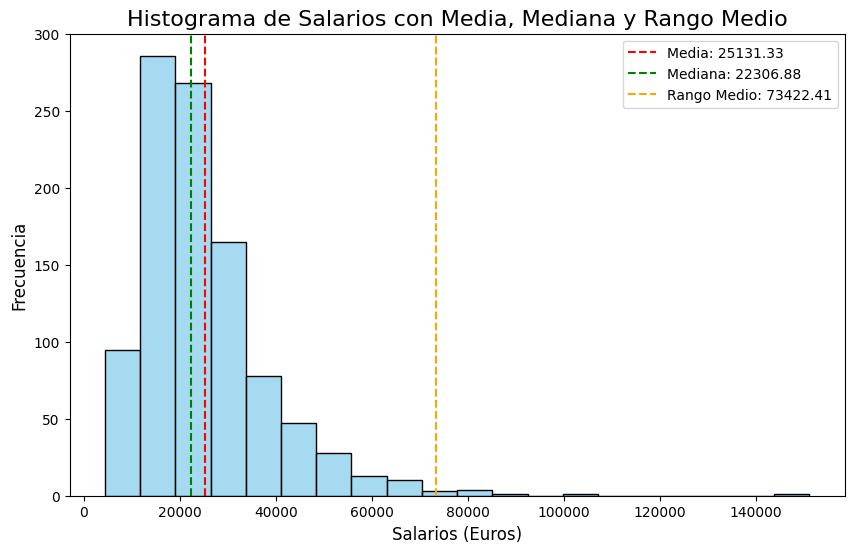
Media: 25131.33
Mediana: 22306.88
Rango medio: 73422.41

Esta distribución, aunque simulada, es bastante parecida a lo que ocurre en la realidad. Los salarios anuales se concentran a la izquierda (salarios bajos), y su frecuencia disminuye rápidamente a medida que nos desplazamos a la derecha, hacia salarios más altos. Es lo conoce como distribución sesgada a la derecha, que vimos por encima al final del segundo artículo de esta serie.

En el extremo derecho, nos econtramos con unos cuantos casos de salarios anuales muy altos (que superan los 100.000 euros).

En este caso, la media aritmética se ha desplazado a la derecha, y es mayor que la mediana. Dicho desplazamiento se debe a la presencia de valores muy altos en el extremo derecho.

Recordemos los valores (redondeados), que hemos obtenido:

Media: 25.131 euros
Mediana: 22.307 euros
Rango medio: 73.4227 euros

Nota: no hemos calculado la moda porque al ser los datos continuos no hay un valor que se repita, y la función de pandas devuelve por defecto el valor mínimo.

df_salarios.head()

	Salarios
0	28236.114017
1	20555.171637
2	30450.091226
3	47170.073204
4	19592.915242

Cualquier empleado sabe que la diferencia entre ganar unos 22.000 euros anuales y unos 25.000 es notoria. El sueldo mensual neto, en el primer caso, ronda los 1.300 euros. En el segundo, los 1.400. Esos 100 euros de más al mes, en sueldos entre los 20.000 y los 30.000 euros brutos anuales, son importantes.

NOTA: Para calcular estos sueldos netos hemos usado la calculadora de Bankinter. Usted puede usar otra obtener métricas ligeramente distintas.

Si en el conjunto de datos se nos colara, por ejemplo, Sundar Pichai, que gana según algunas fuentes consultadas, unos 230 millones de dólares al año (unos 211 millones de euros al cambio, en la fecha de redacción de este artículo), la media aritmética se desplazaría aún más a la derecha. Evidentemente, el sueldo del señor Pichai es un valor atípico extremo y, según los casos, dichos valores deben tratarse de alguna forma. Pero, de nuevo, estamos hablando de algo que no hemos definido aún: valor atípico.

Vamos a dejar esto también para más adelante, para cuando hayamos hablado de las medidas de dispersión y posición. Aquí nos limitaremos a mostrar qué pasa con algunas de las medidas de tendencia central en precencia de valores muy alejados del resto de los datos.

A continuación introduciremos en los datos el sueldo del CEO de Alphabet, y calcularemos de nuevo la media, la mediana y el rango medio:

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Simulación de datos de salarios con más frecuencia en los salarios bajos
np.random.seed(42)  # Para hacer la simulación reproducible
salarios = np.random.lognormal(mean=10, sigma=0.5, size=1000)  # Generar salarios con más concentración en valores bajos

# Incluir un salario de 211 millones
salarios = np.append(salarios, 211000000)  # Añadir salario de 211 millones

# Crear un DataFrame a partir del array de salarios
df_salarios = pd.DataFrame(salarios, columns=['Salarios'])

# Calcular media, mediana y rango medio
media = df_salarios['Salarios'].mean()
mediana = df_salarios['Salarios'].median()
rango_medio = (df_salarios['Salarios'].max() - df_salarios['Salarios'].min()) / 2  # Calcular el rango medio

# Mostrar resultados
print(f'Media: {media:.2f}')
print(f'Mediana: {mediana:.2f}')
print(f'Rango medio: {rango_medio:.2f}')

Media: 235895.43
Mediana: 22315.70
Rango medio: 105497821.88

Con el dato nuevo, el sueldo medio anual es de unos 236.000 euros brutos. A cualquiera que lea esto, le entrará la risa.

Esto pasa porque la media aritmética es muy sensible a los valores extremos, y no siempre podemos eliminar los valores extremos sin más. En estos casos, la mediana es una medida de tendencia central más adecuada, porque es mucho menos sensible a dichos valores.

En el primer conjunto de datos (sin el sueldo atípico), la mediana es de 22.307 euros anuales. En el segundo, de 22.316. Si le decimos a alguien que el «promedio» de los sueldos del conjunto de datos ronda los 22.000 euros, nadie lo tomará como un chiste, y tendrá una idea mucho más cercana a la realidad sobre los salarios.

Si los valores son discretos, o están discretizados, la moda también puede ser una opción. El siguiente código discretiza los datos, agrupando los sueldos en contenedores de ancho de 2.500 euros, y devuelve el rango de sueldos más común:

import numpy as np
import pandas as pd

# Simulación de datos de salarios con más frecuencia en los salarios bajos
np.random.seed(42)  # Para hacer la simulación reproducible
salarios = np.random.lognormal(mean=10, sigma=0.5, size=1000)  # Generar salarios con más concentración en valores bajos

# Añadir un salario outlier de 211 millones
salarios = np.append(salarios, 211_000_000)

# Crear un DataFrame a partir del array de salarios
df_salarios = pd.DataFrame(salarios, columns=['Salarios'])

# Calcular media, mediana y rango medio
media = df_salarios['Salarios'].mean()
mediana = df_salarios['Salarios'].median()
rango_medio = (df_salarios['Salarios'].max() - df_salarios['Salarios'].min()) / 2  # Calcular el rango medio

# Definir el ancho del bin en 2500 euros
ancho_bin = 2500
num_bins = int((df_salarios['Salarios'].max() - df_salarios['Salarios'].min()) / ancho_bin)

# Calcular el rango de sueldos que más se repite
frecuencias, limites = np.histogram(df_salarios['Salarios'], bins=num_bins)
indice_moda = np.argmax(frecuencias)
rango_moda_inferior = limites[indice_moda]
rango_moda_superior = limites[indice_moda + 1]

# Mostrar resultados
print(f'Media: {media:.2f}')
print(f'Mediana: {mediana:.2f}')
print(f'Rango medio: {rango_medio:.2f}')
print(f'Rango de sueldos más frecuente: {rango_moda_inferior:.2f} - {rango_moda_superior:.2f}')

Media: 235895.43
Mediana: 22315.70
Rango medio: 105497821.88
Rango de sueldos más frecuente: 14356.28 - 16856.29

Según estos resultados, el rango de sueldos más común está entre los 14.400 y los 16.900 euros brutos anuales, aproximadamente. Dependiendo de nuestras necesidades de análisis, podemos hacer los rangos más estrechos (de 1.000 euros, por ejemplo), o más anchos (de 5.000, por decir algo). Nadie que vea estos datos los tomará a priori como «disparatados».

Es evidente que el rango medio no es la métrica adecuada en ninguno de los dos casos (con o sin el sueldo del señor Pichai). Afortunadamente, muy pocos usan el rango medio como primera opción para tener una idea del promedio de los datos.

Sin embargo, es frecuente observar casos en los que para describir un conjunto de datos se utiliza la media. Como hemos visto, ésta no siempre es la métrica adecuada. Antes de usarla, es recomendable haberle echado un vistazo previo a los datos.

En conclusión, a veces el problema de las estadísticas no está tanto en su incapacidad de describir la realidad, si no en la métrica que seleccionamos para descirbirla. Otra cosa es que queramos manipular o directamente mentir usando las estadísticas, pero ese es tema para otro artículo.

Bibliografía y referencias

Johnson, R. & Kuby, P. (2008). Estadistica elemental: lo esencial (10a ed.). Cengage Learning Editores S.A.
Freedman, D., Pisani, R., & Purves, R. (2007). Statistics (4a ed.). WW Norton.

Data Science II-B: Estadística descriptiva unidimensional. Medidas de tendencia central

Felipe Maggi

Lenguaje de programación: Python

Media aritmética

Media poblacional

Media muestral

Mediana

Mediana para $n$ impar

Mediana para $n$ par

Cálculo de la mediana con una función paso a paso

Cáculo de la mediana con la función median() de pandas

Moda

Rango medio

Comparativa de medidas de tendencia central y adelanto informal del concepto de distribución normal

Distribución sesgada y adelanto informal del concepto de valores atípicos

Bibliografía y referencias

Contacta

Formulario de contacto de la web datarmony.com	Responder a las personas que nos contactan desde el formulario electrónico de la web.
Cookies, píxel y tracking	Identificar problemas. Obtener datos estadísticos de la navegación de los usuarios. Retener las preferencias del usuario durante su permanencia en un sitio web.
Atención a los derechos de las personas	Atender las solicitudes de los ciudadanos en el ejercicio de los derechos que establece el Reglamento General de Protección de Datos.
Gestión de las comunicaciones recibidas por el canal de denuncias	Crear un canal interno de comunicación para permitir entregar información sobre prácticas irregulares para corregirlas y reparar los daños que hayan podido producir. Proteger a los ciudadanos que informen sobre acciones u omisiones que vulneren el ordenamiento jurídico, afecten a intereses financieros o incidan en el mercado interior.

Felipe Maggi

Lenguaje de programación: Python

Media aritmética

Media poblacional

Media muestral

Mediana

Mediana para n impar

Mediana para n par

Cálculo de la mediana con una función paso a paso

Cáculo de la mediana con la función median() de pandas

Moda

Rango medio

Comparativa de medidas de tendencia central y adelanto informal del concepto de distribución normal

Distribución sesgada y adelanto informal del concepto de valores atípicos

Bibliografía y referencias

Contacta

Mediana para $n$ impar

Mediana para $n$ par