Felipe Maggi
Lenguaje de programación: Python
- Data Science I: Población, muestra, experimentos y tipos de variables.
- Data Science II-A: Estadística descriptiva unidimensional. Tablas de frecuencia y gráficos de distribución.
- Data Science II-B: Estadística descriptiva unidimensional. Medidas de tendencia central.
- Data Science II-C: Estadística descriptiva unidimensional. Medidas de dispersión.
- Data Science II-D: Estadística descriptiva unidimensional. Medidas de posición.
La distribución normal
Repaso de lo que hemos visto hasta ahora
Desde el inicio de esta serie de artículos hemos estado coqueteando con el concepto de normalidad (en la acepción estadística del término), sin llegar a definirlo formalmente. Repasaremos aquí sus apariciones a lo largo de la serie.
Antes de empezar, vamos a recuperar el conjunto de datos simulados con los que hemos estado trabajando desde el principio: las notas obtenidas en todos los exámenes de matemáticas de todos los alumnos de segundo de bachillerato del instituto Luís Vives, durante el año académico 2024-2025.
import pandas as pd
import numpy as np
import random
import string
# Establecer semillas para la reproducibilidad
np.random.seed(42)
random.seed(42)
# Función para generar id_estudiante alfanuméricos aleatorios
def generar_id_estudiante(n):
ids = []
for _ in range(n):
id_estudiante = ''.join(random.choices(string.ascii_uppercase + string.digits, k=8))
ids.append(id_estudiante)
return ids
# Generar datos
num_estudiantes_por_grupo = 40
total_estudiantes = num_estudiantes_por_grupo * 4
num_notas = 10
ids = generar_id_estudiante(total_estudiantes)
asignatura = 'Matemáticas'
temas = [f'Tema {i+1}' for i in range(num_notas)]
fecha_inicio = pd.Timestamp('2024-09-01')
# Función para generar tiempo de estudio con correlación positiva con notas
def generar_tiempo_estudio(notas, media=270, sd=60, correlacion=0.75):
ruido = np.random.normal(0, sd, len(notas))
tiempo_estudio = media + correlacion * (notas - np.mean(notas)) + ruido
return tiempo_estudio.clip(60, 480).astype(int)
# Generar las notas, fechas y otras columnas
data = {
'id_estudiante': [],
'asignatura': [],
'tema': [],
'fecha': [],
'nota': [],
'calificacion': [],
'estatura': [],
'sexo': [],
'tiempo_estudio': [],
'grupo': []
}
# Grupos disponibles
grupos = ['A', 'B', 'C', 'D']
num_grupos = len(grupos)
# Asignar aleatoriamente los estudiantes a los grupos
grupo_asignado = np.repeat(grupos, num_estudiantes_por_grupo)
random.shuffle(grupo_asignado)
for idx, id_estudiante in enumerate(ids):
fechas = [fecha_inicio + pd.DateOffset(weeks=i*4) for i in range(num_notas)]
notas = np.random.normal(6.5, 1, num_notas).clip(0, 10)
estatura = np.random.uniform(150, 190, num_notas)
sexo = random.choice(['H', 'M'])
tiempo_estudio = generar_tiempo_estudio(notas)
for i in range(num_notas):
data['id_estudiante'].append(id_estudiante)
data['asignatura'].append(asignatura)
data['tema'].append(temas[i])
data['fecha'].append(fechas[i])
data['nota'].append(round(notas[i], 2))
# Asignar calificación basada en la nota
if 9 <= notas[i] <= 10:
calificacion = 'sobresaliente'
elif 7 <= notas[i] < 9:
calificacion = 'notable'
elif 5 <= notas[i] < 7:
calificacion = 'aprobado'
else:
calificacion = 'suspenso'
data['calificacion'].append(calificacion)
data['estatura'].append(estatura[i])
data['sexo'].append(sexo)
data['tiempo_estudio'].append(tiempo_estudio[i])
data['grupo'].append(grupo_asignado[idx])
# Crear el DataFrame
df = pd.DataFrame(data)
# Añadir la columna "aprobado"
df['aprobado'] = df['calificacion'].apply(lambda x: 0 if x == 'suspenso' else 1)
# Mostrar el DataFrame
print(df)
id_estudiante asignatura tema fecha nota calificacion \
0 XAJI0Y6D Matemáticas Tema 1 2024-09-01 7.00 aprobado
1 XAJI0Y6D Matemáticas Tema 2 2024-09-29 6.36 aprobado
2 XAJI0Y6D Matemáticas Tema 3 2024-10-27 7.15 notable
3 XAJI0Y6D Matemáticas Tema 4 2024-11-24 8.02 notable
4 XAJI0Y6D Matemáticas Tema 5 2024-12-22 6.27 aprobado
... ... ... ... ... ... ...
1595 FNKOMV2X Matemáticas Tema 6 2025-01-19 4.28 suspenso
1596 FNKOMV2X Matemáticas Tema 7 2025-02-16 7.87 notable
1597 FNKOMV2X Matemáticas Tema 8 2025-03-16 5.41 aprobado
1598 FNKOMV2X Matemáticas Tema 9 2025-04-13 7.76 notable
1599 FNKOMV2X Matemáticas Tema 10 2025-05-11 7.45 notable
estatura sexo tiempo_estudio grupo aprobado
0 157.272999 H 357 C 1
1 157.336180 H 256 C 1
2 162.169690 H 274 C 1
3 170.990257 H 185 C 1
4 167.277801 H 236 C 1
... ... ... ... ... ...
1595 173.907293 M 252 A 0
1596 184.787835 M 250 A 1
1597 185.633286 M 299 A 1
1598 167.961510 M 189 A 1
1599 168.372148 M 284 A 1
[1600 rows x 11 columns]
media_nota = df["nota"].mean()
var_nota = df["nota"].var()
print('nota media =',round(media_nota, 2))
print('varianza notas =',round(var_nota, 2))
nota media = 6.48 varianza notas = 1.03
import seaborn as sns
import matplotlib.pyplot as plt
# Graficar la densidad de las notas usando Seaborn (población=
plt.figure(figsize=(10, 6))
sns.kdeplot(data=df['nota'], fill=True, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Densidad')
plt.show()
Al final del segundo artículo vimos brevemente algunos tipos de distribuciones comunes, siendo la distribución normal la primera de ellas. Ahí sí la nombramos, y mencionamos su parecido a una campana. En este caso, en lugar de un gráfico de densidad usamos un histograma con 11 contenedores, donde la altura de cada contenedor representa el número de observaciones que hay dentro de ellos, y pintamos la curva de densidad encima del gráfico:
# Graficar el histograma con 11 contenedores sin forzar bordes específicos
plt.figure(figsize=(10, 6))
sns.histplot(data=df['nota'], bins=11, kde=True, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.show()
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statistics
# Establecer semillas para la reproducibilidad
np.random.seed(42)
random.seed(42)
# Función para calcular la moda usando pandas
def calcular_moda_pandas(df):
return df['nota'].mode()[0]
# Función para calcular el rango medio
def calcular_rango_medio(df):
minimo = df['nota'].min()
maximo = df['nota'].max()
return (minimo + maximo) / 2
# Crear la gráfica de densidad de las notas y marcar media, mediana, moda y rango medio
def graficar_densidad(df):
# Calcular estadísticas
media = df['nota'].mean()
mediana = df['nota'].median()
moda = calcular_moda_pandas(df)
rango_medio = calcular_rango_medio(df)
# Crear la gráfica de densidad
plt.figure(figsize=(10, 6))
sns.kdeplot(df['nota'], fill=True, color='blue', label='Densidad')
# Marcar la media
plt.axvline(media, color='red', linestyle='-', label=f'Media: {media:.2f}')
# Marcar la mediana
plt.axvline(mediana, color='green', linestyle='--', label=f'Mediana: {mediana:.2f}')
# Marcar la moda
plt.axvline(moda, color='purple', linestyle='--', label=f'Moda: {moda:.2f}')
# Marcar el rango medio
plt.axvline(rango_medio, color='orange', linestyle='--', label=f'Rango medio: {rango_medio:.2f}')
# Etiquetas y título
plt.title('Densidad de Notas con Media, Mediana, Moda y Rango Medio')
plt.xlabel('Notas')
plt.ylabel('Densidad')
plt.legend()
# Personalizar los ticks del eje x para mostrar solo los valores 2 a 9
plt.xticks([2, 3, 4, 5, 6, 7, 8, 9])
# Mostrar la gráfica
plt.show()
# Llamada a la función
graficar_densidad(df)
«Las notas tienen una distribución que parece una campana. Los valores se concentran en torno a las medidas de tendencia central, y son menos frecuentes (tienen menor densidad) en los extremos«.
En este artículo veremos que esto último es lo que se conoce como simetría. Una distribución normal es simétrica con respecto a la media, pero no nos adelantemos.
Tras haber estudiado las medidas de dispersión, en el cuarto artículo, y las de posición, junto con el concepto de calificación estándar (o $Z$), en el quinto, ya pudimos ofrecer una definición empírica de normalidad:
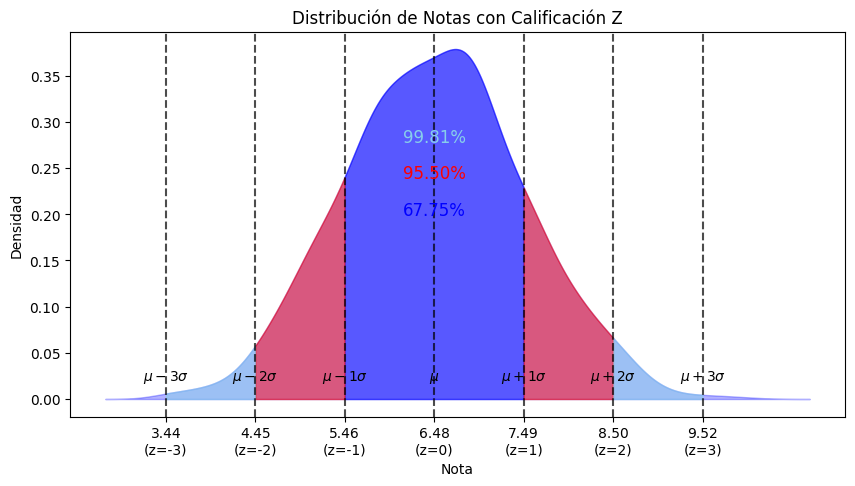
«Si una variable está normalmente distribuida, entonces (1) dentro de una desviación estándar de la media habrá aproximadamente un 68% de los datos; (2) dentro de dos desviaciones estándar de la media habrá aproximadamente un 95% de los datos; y (3) dentro de tres desviaciones estándar de la media habrá aproximadamente un 99.7% de los datos» (Johnson & Kuby, 2008).
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
# Calcular la media y la desviación estándar de la variable "nota"
media_nota = df["nota"].mean()
std_nota = df["nota"].std()
# Calcular los porcentajes reales de datos dentro de 1, 2 y 3
# desviaciones estándar
z1 = ((df["nota"] >= media_nota - std_nota) &
(df["nota"] <= media_nota + std_nota)).mean() * 100
z2 = ((df["nota"] >= media_nota - 2 * std_nota) &
(df["nota"] <= media_nota + 2 * std_nota)).mean() * 100
z3 = ((df["nota"] >= media_nota - 3 * std_nota) &
(df["nota"] <= media_nota + 3 * std_nota)).mean() * 100
# Crear los datos de la densidad
kde = sm.nonparametric.KDEUnivariate(df["nota"])
kde.fit()
x_kde = kde.support
y_kde = kde.density
# Crear el gráfico de densidad
plt.figure(figsize=(10, 5))
plt.fill_between(x_kde, y_kde, color="blue", alpha=0.3)
def shade_region(start, end, color):
mask = (x_kde >= start) & (x_kde <= end)
plt.fill_between(x_kde[mask], y_kde[mask], color=color, alpha=0.5)
# Sombrear las áreas correspondientes
shade_region(media_nota - std_nota, media_nota + std_nota, "blue") # 1σ
shade_region(media_nota - 2 * std_nota, media_nota - std_nota, "red")
shade_region(media_nota + std_nota, media_nota + 2 * std_nota, "red") # 2σ
shade_region(media_nota - 3 * std_nota, media_nota - 2 * std_nota, "skyblue")
shade_region(media_nota + 2 * std_nota, media_nota + 3 * std_nota, "skyblue") # 3σ
# Marcar la media y las desviaciones estándar
for i in range(-3, 4):
valor = media_nota + i * std_nota
etiqueta = "$\\mu$" if i == 0 else f"$\\mu {'+' if i > 0 else '-'} {abs(i)}\\sigma$"
plt.axvline(valor, color="black", linestyle="--", alpha=0.7)
plt.text(valor, plt.ylim()[1] * 0.05,
etiqueta,
horizontalalignment='center',
color="black")
# Agregar los valores de calificación z debajo del eje x
ticks_x = [media_nota + i * std_nota for i in range(-3, 4)]
labels_x = [f"{tick:.2f}\n(z={i})" for i, tick in zip(range(-3, 4), ticks_x)]
plt.xticks(ticks_x, labels_x)
# Agregar porcentajes reales en la parte superior
plt.text(media_nota, plt.ylim()[1] * 0.5, f"{z1:.2f}%",
horizontalalignment='center', fontsize=12, color="blue")
plt.text(media_nota, plt.ylim()[1] * 0.6, f"{z2:.2f}%",
horizontalalignment='center', fontsize=12, color="red")
plt.text(media_nota, plt.ylim()[1] * 0.7, f"{z3:.2f}%",
horizontalalignment='center', fontsize=12, color="skyblue")
# Etiquetas y título
plt.xlabel("Nota")
plt.ylabel("Densidad")
plt.title("Distribución de Notas con Calificación Z")
plt.show()
La distribución teórica
Todo esto tiene sentido porque existe una distribución teórica «normal», contra la que podemos comparar los datos de las notas. El siguiente código hace esto por nosotros:
import pandas as pd
import numpy as np
# Calcular media y desviación estándar de las notas
media_nota = df["nota"].mean()
std_nota = df["nota"].std()
# Contar valores dentro de 1, 2 y 3 desviaciones estándar
dentro_1std = ((df["nota"] >= media_nota - std_nota) & (df["nota"] <= media_nota + std_nota)).mean() * 100
dentro_2std = ((df["nota"] >= media_nota - 2 * std_nota) & (df["nota"] <= media_nota + 2 * std_nota)).mean() * 100
dentro_3std = ((df["nota"] >= media_nota - 3 * std_nota) & (df["nota"] <= media_nota + 3 * std_nota)).mean() * 100
# Valores teóricos en distribución normal
teorico_1std = 68.27
teorico_2std = 95.45
teorico_3std = 99.73
# Crear DataFrame de comparación
comparacion_df = pd.DataFrame({
"Rango": ["Media ± 1σ", "Media ± 2σ", "Media ± 3σ"],
"Real (%)": [dentro_1std, dentro_2std, dentro_3std],
"Teórico (%)": [teorico_1std, teorico_2std, teorico_3std]
})
# Mostrar la tabla
print(comparacion_df)
Rango Real (%) Teórico (%) 0 Media ± 1σ 67.7500 68.27 1 Media ± 2σ 95.5000 95.45 2 Media ± 3σ 99.8125 99.73
Pero la pregunta que todo buen analista debe hacerse, llegados a este punto, es ¿de dónde sale esa distribución teórica? Aquí las cosas se complican un poco, matemáticamente hablando.
Es importante decir que la distribución normal, de Gauss, gaussiana o de Laplace-Gauss se usa con variables continuas, pero es muy frecuente aproximar esta distribución cuando se trabaja con variables discretas, tal y como hemos visto en artículos anteriores, o en este mismo artículo cuando hemos discretizado las notas para hacer un histograma, sobre el que hemos dibujado una curva de densidad. Dicho esto entremos en materia, en la medida de nuestras capacidades.
En la naturaleza se dan muchos ejemplos en los que los fenómenos se distribuyen de forma que los datos se concentran en torno a las medidas centrales, y son menos frecuentes en los extremos. Tanto es así, que de ahí viene el adjetivo de «normal».
El primero que presentó este tipo de distribución fue de Moivre en 1733, «en el contexto de cierta aproximación de la distribución binomial, para grandes valores de n» (Wikipedia).
Posteriormente, Laplace amplió los resultados de Moivre, aplicándlos en el análisis de errores de experimentos. Gauss, por su parte, llegó a la distribución normal, al parecer de forma independiente de Moivre, analizando datos astronómicos.
No entraremos en los detalles del proceso matemático a partir del cual se deriva la función de densidad normal. Lo que sí diremos es que, como en muchos otros ejemplos de avances científicos, la observación de datos reales, ya sean errores aleatorios en experimentos, ya sean datos astronómicos, permitió aproximar una función de densidad que se ajustaba mucho a los datos observados.
Esa función es la que permite calcular los porcentajes teóricos de datos a 1, 2 y 3 desviaciones estándar de la media. Evidentemente, la función «pinta» una curva perfecta, y los datos reales se aproximan a esa curva. Pero la aproximación es lo suficientemente buena como para poder extrapolar los datos de una muestra a una población general, una vez comprobamos (o asumimos), que la distribución de la población analizada es normal.
Formulación matemática
Llegados aquí, lo lógico es mostrar la fórmula de la función de densidad normal que, como decimos, deriva de los trabajos de Moivre, Laplace y Gauss:
$$f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
Donde:
- $\mu$ es la media
- $\sigma^2$ es la varianza
- $\sigma$ es la desviación típica
- media = 6.48,
- varianza = 1.03.
Recordemos que al inicio de este artículo calculamos la media y la varianza de la población de notas, y esos eran los valores que obtuvimos.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# --- 1. Definir los parámetros ---
# Media de la distribución
mu = 6.48
# Varianza de la distribución
variance = 1.03
# La desviación estándar es la raíz cuadrada de la varianza
sigma = np.sqrt(variance)
# --- 2. Preparar los datos para el gráfico ---
# Creamos un rango de valores para el eje X.
# Usamos de -4 a +4 desviaciones estándar alrededor de la media para cubrir la mayor parte de la curva.
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
# Calculamos los valores del eje Y usando la función de densidad de probabilidad (PDF) de SciPy.
y = norm.pdf(x, mu, sigma)
# --- 3. Crear el gráfico ---
# Configuramos el tamaño de la figura para que se vea bien
plt.figure(figsize=(10, 6))
# Dibujamos la curva
plt.plot(x, y, color='#007acc', linewidth=2, label=f'σ² = {variance:.2f}')
# Añadimos una línea vertical para marcar la media (μ)
plt.axvline(mu, color='red', linestyle='--', linewidth=1.5, label=f'Media (μ) = {mu}')
# --- 4. Añadir títulos y etiquetas ---
plt.title(f'Distribución Normal (μ = {mu}, σ² = {variance})', fontsize=16)
plt.xlabel('Valor', fontsize=12)
plt.ylabel('Densidad de Probabilidad', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.6)
plt.legend()
# --- 5. Mostrar el gráfico ---
plt.show()
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import norm
def graficar_densidad_comparativa(df, mu_teorica, varianza_teorica):
"""
Grafica la densidad de los datos reales de la columna 'nota' y la compara
con una distribución normal teórica.
Args:
df (pd.DataFrame): DataFrame con la columna 'nota'.
mu_teorica (float): Media para la curva normal teórica.
varianza_teorica (float): Varianza para la curva normal teórica.
"""
# --- 1. Calcular estadísticas de los datos REALES ---
notas_reales = df['nota']
media_real = notas_reales.mean()
mediana_real = notas_reales.median()
# --- 2. Preparar la gráfica ---
plt.figure(figsize=(12, 7))
# Dibuja la curva de densidad de los datos REALES
sns.kdeplot(notas_reales, fill=True, color='#2b7bba', label='Densidad de Datos Reales')
# Añade líneas para la media y mediana REALES
plt.axvline(media_real, color='#e63946', linestyle='-', linewidth=2, label=f'Media Real: {media_real:.2f}')
plt.axvline(mediana_real, color='#52b788', linestyle='--', linewidth=2, label=f'Mediana Real: {mediana_real:.2f}')
# --- 3. Superponer la curva de la distribución normal TEÓRICA ---
# Calcula la desviación estándar teórica
sigma_teorica = np.sqrt(varianza_teorica)
# Crea un rango de valores X que cubra la gráfica
xmin, xmax = plt.xlim()
x_teorico = np.linspace(xmin, xmax, 1000)
# Calcula los valores Y para la curva teórica
y_teorico = norm.pdf(x_teorico, mu_teorica, sigma_teorica)
# Dibuja la curva teórica
plt.plot(x_teorico, y_teorico, color='black', linestyle='-.', linewidth=2.5, label='Normal Teórica (μ=6.48, σ²=1.03)')
# --- 4. Personalizar y mostrar el gráfico ---
plt.title('Comparativa: Densidad Real vs. Distribución Normal Teórica', fontsize=16)
plt.xlabel('Notas', fontsize=12)
plt.ylabel('Densidad', fontsize=12)
plt.legend()
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
# 2. Llama a la función con tu df y los parámetros teóricos
graficar_densidad_comparativa(df, mu_teorica=6.48, varianza_teorica=1.03)
Ahora bien, ¿cómo se calculan en la práctica esos porcentajes? Aquí debemos ampliar el aparato matemático, y hablar de la función de distribución.
Esto es adelantarse un poco (o bastante), porque aún no hemos entrado en el terreno de la probabilidad de forma seria. Sin embargo, en los primeros artículos rozamos el concepto cuando hablamos de la probabilidad de sacar un 8.45, o la probabilidad de sacar una nota superior a 8.0. Esta probabilidad es equivalente al porcentaje de notas iguales a 8.45, en el primer caso, y equivalente al porcentaje de notas superiores a 8.0, en el segundo.
Es decir, y si recordamos lo que vimos en el segundo artículo, en que estudiamos las tablas de distribución o frecuencia, la probalidad de obtener una nota concreta es igual a la frecuencia relativa de dicha nota en el conjunto de datos. La probabilidad de que la nota sea igual o inferior a una dada, es la fecuencia relativa acumulada de esa nota.
Estadística y probabilidad están íntimamente relacionadas, y lo que nos da la función de distribución es la probabilidad de obtener un valor que está entre dos valores determinados, o que sea inferior o superior a un valor dado.
Si discretizamos las notas, aproximar esas probabilidades es relativamente sencillo. Revisemos de nuevo el histograma de las notas, pero ligeramente alterado para facilitar los cálculos:
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
# 1. Definición de los bordes de los contenedores
# np.arange(12) crea un array [0, 1, 2, ..., 11] para 11 contenedores
bin_edges = np.arange(12)
# 2. Creación del gráfico
plt.figure(figsize=(10, 6))
# Se asigna el gráfico a la variable 'ax' para poder manipular sus elementos
# NOTA: Asegúrate de que tu DataFrame se llame 'df' y tenga la columna 'nota'
ax = sns.histplot(data=df['nota'], bins=bin_edges, kde=False, color='blue')
# 3. Configuración de títulos y ejes
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.xticks(bin_edges) # Asegura que los ticks del eje X coincidan con los bordes
# 4. Bucle para añadir las etiquetas de frecuencia sobre cada barra
for p in ax.patches:
height = p.get_height()
if height > 0:
ax.text(
x=p.get_x() + p.get_width() / 2., # Posición X (centro de la barra)
y=height + 2, # Posición Y (un poco encima de la barra)
s=f'{int(height)}', # Texto a mostrar (frecuencia)
ha='center' # Alineación horizontal
)
# 5. Mostrar el gráfico final
plt.show()
Es importante saber que, por defecto, los contenedores se construyen de esta forma: $[a,b)$, lo que significa que el primer número está en el contenedor, y el segundo no (que está incluido en el contenedor siguiente).
Por lo tanto, y por ejemplo, en el contenedor que va de 8 a 9, el 8 está, pero en el 9 no. Pero si hubiese un 8.99, sí estaría en dicho contenedor.
Esto explica porqué hay un contenedor que va de 10 a 11, aunque la nota máxima es 10. El único 10 que hay en el conjunto de datos está en ese contenedor.
Una vez aclarado esto, podemos decir que entre 8 y 9 (entre 8.00, y 8.99), hay 108 notas.
Sabemos que el número total de notas es 1600, por lo que la probabilidad de meter la mano en una bolsa con todas las notas, y sacar una entre 8.00 y 8.99 es de
$108/1600 = 0.0675$ (o 6.75% si lo expresamos en porcentajes).
La probabilidad de sacar una nota inferior a 9 es equivalente a la suma de probabilidades de sacar una nota entre entre 0 y 1, 2 y 3, 3 y 4, 5 y 6 y así hasta 8 y 9:
$(0+0+0+10+112+401+595+365+108)/1600 = 0.9944$
Es decir, la probabilidad de sacar de la bolsa una nota inferior a 9 es de un 99.44%
Si en lugar de mostrar la frecuencia de las notas que caen en cada contenedor mostramos directamente su porcentaje, los cálculos son todavía más sencillos:
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
from matplotlib.ticker import PercentFormatter
# (Asegúrate de que tu DataFrame 'df' ya esté cargado aquí)
# 1. Definición de los bordes de los contenedores
bin_edges = np.arange(12)
# 2. Creación del gráfico
plt.figure(figsize=(10, 6))
# Se añade stat='percent' para que el eje Y muestre porcentajes
ax = sns.histplot(data=df['nota'], bins=bin_edges, stat='percent', kde=False, color='blue')
# 3. Configuración de títulos y ejes
plt.title('Distribución de Notas de la Población (%)')
plt.xlabel('Nota')
plt.ylabel('Porcentaje (%)') # Etiqueta del eje Y actualizada
plt.xticks(bin_edges)
# 4. Bucle para añadir las etiquetas de porcentaje sobre cada barra
for p in ax.patches:
height = p.get_height() # La altura ahora es un porcentaje
if height > 0:
ax.text(
x=p.get_x() + p.get_width() / 2.,
y=height + 0.2, # Se ajusta el offset para la nueva escala
s=f'{height:.2f}%', # Se formatea como texto de porcentaje con 1 decimal
ha='center'
)
# 5. Mostrar el gráfico final
plt.show()
Es sencillo extrapolar dicha densidad al concepto de probabilidad. Sacar de una bolsa que contiene todas las notas del conjunto de datos, una nota que esté entre 8 y 9 (entre 8.00 y 8.99), es igual al ancho del contenedor por su altura: 1 x 6.75%.
Atención: ancho por altura es un área. Así que podemos decir que la probabilidad de obtener una nota entre 8.00 y 8.99 es igual al área del contenedor correspondiente.
El problema de este acercamiento es que, para hacer sencillos los cálculos, hemos perdido cierta rigurosidad… Los contenedores no están hechos de forma que sus límites coincidan con las desviaciones estándar por encima y por debajo de la media.
Esto podemos justificarlo diciendo que, haciendo eso, la interpretación de los datos es más compleja si lo que queremos es hacer un informe sobre la distribución de notas para los responsables del departamento de matemáticas.
Pero si lo que queremos es justificar de dónde salen los porcentajes teóricos de una distribución normal entonces vale la pena el ejercicio. El siguiente código muestra la distribución de notas de forma que los límites de los contenedores coinciden con la nota media, y con las notas que está 1, 2 y 3 desviaciones estándar de esa media.
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
# 1. Calcular la media y la desviación estándar
media = df['nota'].mean()
desviacion_estandar = df['nota'].std()
# 2. Definir los bordes de los contenedores
bin_edges = [
media - 3 * desviacion_estandar,
media - 2 * desviacion_estandar,
media - 1 * desviacion_estandar,
media,
media + 1 * desviacion_estandar,
media + 2 * desviacion_estandar,
media + 3 * desviacion_estandar
]
# 3. Crear las etiquetas personalizadas para el eje X
# Se usa \n para crear un salto de línea entre la etiqueta sigma y el valor
tick_labels = [
f'μ-3σ\n({bin_edges[0]:.2f})',
f'μ-2σ\n({bin_edges[1]:.2f})',
f'μ-1σ\n({bin_edges[2]:.2f})',
f'μ\n({bin_edges[3]:.2f})',
f'μ+1σ\n({bin_edges[4]:.2f})',
f'μ+2σ\n({bin_edges[5]:.2f})',
f'μ+3σ\n({bin_edges[6]:.2f})'
]
# 4. Creación del gráfico
plt.figure(figsize=(12, 7))
ax = sns.histplot(data=df['nota'], bins=bin_edges, stat='percent', kde=False, color='blue')
# 5. Configuración de títulos y ejes
plt.title('Distribución de Notas por Desviación Estándar (%)')
plt.xlabel('Nota (Agrupada por Desviación Estándar)')
plt.ylabel('Porcentaje (%)')
# Se usan las nuevas etiquetas personalizadas en el eje X
plt.xticks(ticks=bin_edges, labels=tick_labels)
# 6. Bucle para añadir las etiquetas de porcentaje sobre cada barra
for p in ax.patches:
height = p.get_height()
if height > 0:
ax.text(
x=p.get_x() + p.get_width() / 2.,
y=height + 0.2,
s=f'{height:.2f}%',
ha='center'
)
# 7. Asegurar que todo el gráfico sea visible
plt.tight_layout()
# 8. Mostrar el gráfico final
plt.show()
NOTA: las pequeñas diferencias con los datos obtenidos anteriormente se explican por cómo hemos construido los contenedores.
Visto todo esto, volvamos a la curva teórica. Calcular áreas de contenedores rectangulares, como hemos hecho hasta ahora, es muy fácil. Pero el tema se complica si lo que tenemos entre manos es una curva.
La curva normal se aplica cuando los datos son variables continuas (o cuando tratamos las variables como continuas –ver el primer artículo de esta serie-).
Recordemos que la función de densidad de una distribución normal es:
$$f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
Recordemos también que el resultado para una media de 6.48 y una varianza de 1.03 es:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# --- 1. Definir los parámetros ---
# Media de la distribución
mu = 6.48
# Varianza de la distribución
variance = 1.03
# La desviación estándar es la raíz cuadrada de la varianza
sigma = np.sqrt(variance)
# --- 2. Preparar los datos para el gráfico ---
# Creamos un rango de valores para el eje X.
# Usamos de -4 a +4 desviaciones estándar alrededor de la media para cubrir la mayor parte de la curva.
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
# Calculamos los valores del eje Y usando la función de densidad de probabilidad (PDF) de SciPy.
y = norm.pdf(x, mu, sigma)
# --- 3. Crear el gráfico ---
# Configuramos el tamaño de la figura para que se vea bien
plt.figure(figsize=(10, 6))
# Dibujamos la curva
plt.plot(x, y, color='#007acc', linewidth=2, label=f'σ² = {variance:.2f}')
# Añadimos una línea vertical para marcar la media (μ)
plt.axvline(mu, color='red', linestyle='--', linewidth=1.5, label=f'Media (μ) = {mu}')
# --- 4. Añadir títulos y etiquetas ---
plt.title(f'Distribución Normal (μ = {mu}, σ² = {variance})', fontsize=16)
plt.xlabel('Valor', fontsize=12)
plt.ylabel('Densidad de Probabilidad', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.6)
plt.legend()
# --- 5. Mostrar el gráfico ---
plt.show()
En su lugar, debemos recurrir a las integrales, y a lo que se conoce como la función de distribución que mencionábamos antes. La siguiente integral nos da el área bajo la curva entre menos infinito y un valor de $x$:
$$F(x) = \int_{-\infty}^{x} \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(u-\mu)^{2}}{2\sigma^{2}}} du$$
A estas alturas ya deberíamos poder ver que esa área es la probabilidad de obtener una nota inferior o igual a $x$:
$$F(x) = P(X \le x)$$
A continuación , presentamos a modo de ejemplo, un gráfico de la distribución teórica de las notas (con media 6.48 y varianza 1.03) con el área sombreada entre $-\infty$ y $7.00$
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# --- 1. Definir los parámetros ---
# Media de la distribución
mu = 6.48
# Varianza de la distribución
variance = 1.03
# La desviación estándar es la raíz cuadrada de la varianza
sigma = np.sqrt(variance)
x_limite = 7 # El valor de X hasta donde se sombreará el área
# --- 2. Generar datos para la curva ---
# Crear un rango de valores de X para graficar la curva completa
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
# Calcular los valores de Y (densidad de probabilidad) para cada X
y = norm.pdf(x, mu, sigma)
# --- 3. Crear la gráfica ---
fig, ax = plt.subplots(figsize=(10, 6))
# Dibujar la curva de distribución normal
ax.plot(x, y, 'b-', linewidth=2, label='Curva Normal')
# --- 4. Sombrear el área bajo la curva ---
# Definir el rango de X para el área sombreada (desde el inicio hasta x_limite)
x_fill = np.linspace(mu - 4*sigma, x_limite, 1000)
# Calcular los valores de Y correspondientes
y_fill = norm.pdf(x_fill, mu, sigma)
# Rellenar el área
ax.fill_between(x_fill, y_fill, color='skyblue', alpha=0.6, label=f'Área para X ≤ {x_limite}')
# --- 5. Añadir detalles y personalizar la gráfica ---
# Calcular la probabilidad (área sombreada)
probabilidad = norm.cdf(x_limite, mu, sigma)
# Añadir título y etiquetas
ax.set_title(f'Distribución Normal (μ={mu}, σ² = {variance})', fontsize=16)
ax.set_xlabel('Valores de X', fontsize=12)
ax.set_ylabel('Densidad de Probabilidad', fontsize=12)
# Añadir una línea vertical en X = 7
ax.axvline(x=x_limite, color='red', linestyle='--', label=f'X = {x_limite}')
# Añadir texto con el valor de la probabilidad
ax.text(mu - 3.5*sigma, max(y)*0.6, f'P(X ≤ {x_limite}) = {probabilidad:.4f}',
fontsize=14, bbox=dict(facecolor='white', alpha=0.8))
# Añadir una leyenda y una cuadrícula
ax.legend()
ax.grid(True, linestyle='--', alpha=0.6)
# Mostrar la gráfica
plt.show()
Ahora vamos a cerrar el círculo, para responder a la pregunta aquella que hacíamos antes… ¿De dónde salen los porcentajes teóricos de concentración de datos a 1, 2 y 3 desviaciones estándar de la media?
Pues de esta distribución normal teórica, evidentemente. Lo vamos a mostrar calculando la integral entre 5.46 y 7.49 (una desviación estándar por arriba y abajo de la media)
Como ejercicio se puede hacer lo mismo para dos y tres desviaciones estándar por encima de la media.
Recordemos antes cómo es la distribución real de las notas, y los valores que marcan los límites a 1, y 2 y 3 desviaciones estándar:
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
# Calcular la media y la desviación estándar de la variable "nota"
media_nota = df["nota"].mean()
std_nota = df["nota"].std()
# Calcular los porcentajes reales de datos dentro de 1, 2 y 3
# desviaciones estándar
z1 = ((df["nota"] >= media_nota - std_nota) &
(df["nota"] <= media_nota + std_nota)).mean() * 100
z2 = ((df["nota"] >= media_nota - 2 * std_nota) &
(df["nota"] <= media_nota + 2 * std_nota)).mean() * 100
z3 = ((df["nota"] >= media_nota - 3 * std_nota) &
(df["nota"] <= media_nota + 3 * std_nota)).mean() * 100
# Crear los datos de la densidad
kde = sm.nonparametric.KDEUnivariate(df["nota"])
kde.fit()
x_kde = kde.support
y_kde = kde.density
# Crear el gráfico de densidad
plt.figure(figsize=(10, 5))
plt.fill_between(x_kde, y_kde, color="blue", alpha=0.3)
def shade_region(start, end, color):
mask = (x_kde >= start) & (x_kde <= end)
plt.fill_between(x_kde[mask], y_kde[mask], color=color, alpha=0.5)
# Sombrear las áreas correspondientes
shade_region(media_nota - std_nota, media_nota + std_nota, "blue") # 1σ
shade_region(media_nota - 2 * std_nota, media_nota - std_nota, "red")
shade_region(media_nota + std_nota, media_nota + 2 * std_nota, "red") # 2σ
shade_region(media_nota - 3 * std_nota, media_nota - 2 * std_nota, "skyblue")
shade_region(media_nota + 2 * std_nota, media_nota + 3 * std_nota, "skyblue") # 3σ
# Marcar la media y las desviaciones estándar
for i in range(-3, 4):
valor = media_nota + i * std_nota
etiqueta = "$\\mu$" if i == 0 else f"$\\mu {'+' if i > 0 else '-'} {abs(i)}\\sigma$"
plt.axvline(valor, color="black", linestyle="--", alpha=0.7)
plt.text(valor, plt.ylim()[1] * 0.05,
etiqueta,
horizontalalignment='center',
color="black")
# Agregar los valores de calificación z debajo del eje x
ticks_x = [media_nota + i * std_nota for i in range(-3, 4)]
labels_x = [f"{tick:.2f}\n(z={i})" for i, tick in zip(range(-3, 4), ticks_x)]
plt.xticks(ticks_x, labels_x)
# Agregar porcentajes reales en la parte superior
plt.text(media_nota, plt.ylim()[1] * 0.5, f"{z1:.2f}%",
horizontalalignment='center', fontsize=12, color="blue")
plt.text(media_nota, plt.ylim()[1] * 0.6, f"{z2:.2f}%",
horizontalalignment='center', fontsize=12, color="red")
plt.text(media_nota, plt.ylim()[1] * 0.7, f"{z3:.2f}%",
horizontalalignment='center', fontsize=12, color="skyblue")
# Etiquetas y título
plt.xlabel("Nota")
plt.ylabel("Densidad")
plt.title("Distribución de Notas con Calificación Z")
plt.show()
$$F(x) = \int_{5.46}^{7.49} \frac{1}{1.01\sqrt{2\pi}} e^{-\frac{(u-6.48)^{2}}{2*1.03}} du$$
Importante: en esta fórmula, las expresiones de media, varianza y desviación estándar están aproximadas. En el código siguiente, el valor de la integral se calcula con la función norm.pdf, de la librería scipy.stats (que es un enfoque mucho más eficiente que calcular la integral propiamente dicha).
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# --- 1. Definir los parámetros ---
# Media de la distribución
mu = 6.48
# Varianza de la distribución
variance = 1.03
# La desviación estándar es la raíz cuadrada de la varianza
sigma = np.sqrt(variance)
# Límites para la integración y el sombreado
x1 = 5.46
x2 = 7.49
# --- 2. Calcular la probabilidad (Integral) ---
# La probabilidad P(x1 < X < x2) es la diferencia de las funciones de distribución acumulada (CDF)
probabilidad = norm.cdf(x2, mu, sigma) - norm.cdf(x1, mu, sigma)
print(f"El valor de la integral entre {x1} y {x2} es: {probabilidad:.4f}")
# --- 3. Generar datos para la curva ---
# Crear un rango de valores de X para graficar la curva completa
x_curve = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
# Calcular los valores de Y (densidad de probabilidad) para cada X
y_curve = norm.pdf(x_curve, mu, sigma)
# --- 4. Crear la gráfica ---
fig, ax = plt.subplots(figsize=(12, 7))
# Dibujar la curva de distribución normal
ax.plot(x_curve, y_curve, 'b-', linewidth=2, label='Curva Normal')
# --- 5. Sombrear el área bajo la curva entre x1 y x2 ---
# Definir el rango de X para el área sombreada
x_fill = np.linspace(x1, x2, 1000)
# Calcular los valores de Y correspondientes
y_fill = norm.pdf(x_fill, mu, sigma)
# Rellenar el área
ax.fill_between(x_fill, y_fill, color='skyblue', alpha=0.7, label=f'Área entre {x1} y {x2}')
# --- 6. Añadir detalles y personalizar la gráfica ---
# Añadir título y etiquetas
ax.set_title(f'Distribución Normal (μ={mu}, σ²={variance})', fontsize=16)
ax.set_xlabel('Valores de X', fontsize=12)
ax.set_ylabel('Densidad de Probabilidad', fontsize=12)
# Añadir líneas verticales en los límites de la integral
ax.axvline(x=x1, color='red', linestyle='--', label=f'Límite inferior: {x1}')
ax.axvline(x=x2, color='green', linestyle='--', label=f'Límite superior: {x2}')
# Añadir texto con el valor de la probabilidad
ax.text(x_curve.min(), max(y_curve)*0.7, f'P({x1} ≤ X ≤ {x2}) = {probabilidad:.4f}',
fontsize=14, bbox=dict(facecolor='white', alpha=0.9))
# Añadir una leyenda y una cuadrícula
ax.legend()
ax.grid(True, linestyle='--', alpha=0.6)
# Guardar y mostrar la gráfica
plt.savefig("distribucion_normal_area.png")
plt.show()
La ventaja de usar la teoría, en lugar de las distribuciones reales, es que los cálculos se simplifican mucho. Una vez se establece que una distribución es aproximadamente normal, en lugar de calcular integrales de la función «real», podemos hacerlo con la distribución téorica, solo conociendo la media y la varianza de los datos reales.
Esto último era especialmente cierto en tiempos de Moivre, Laplace y Gauss, en los que no existía Python o cualquier otra herramienta similar para graficar funciones, y calcular integrales, y era mucho más sencillo recurrir a tablas prefabricadas en función de los datos teóricos.
Medidas de forma y concentración
En artículos anteriores revisamos las medidas de tendencia central, de posición y de dispersión. Ahora, tras haber estudiado la distribución normal, podemos revisar los conceptos de asimetría o sesgo, y de curtosis o apuntamiento.
La asimetría
La asimetría o sesgo es un estadistico que indica, en palabras de Dolores Lorente «cómo es la forma de la distribución con respecto a la media artimética» (o eje de asimetría).
Se suele hallar mediante el coeficiente de asimetría de Fischer (CAF):
$$CA_F = \frac{\sum_{i=1}^{N}(x_i – \bar{x})^3}{N \cdot \sigma^3}$$
- Asimetría negativa o a la izquierda: coeficiente negativo ($CA_F < 0$)
- Simétrica: coeficiente igual a cero ($CA_F = 0$)
- Asimetría positiva o a la derecha: coeficiente positivo ($CA_F > 0$)
Evidentemente, y como adelantamos antes, la distribución normal, que es simétrica con respecto a la media aritmética, tiene un coeficiente de simetría nulo ($CA_F = 0$).
En el primer artículo ya vimos ejemplos de distribuciones asimétricas:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generar datos con distribución exponencial y luego invertirlos para sesgo a la izquierda
data_sesgada_izquierda = -np.random.exponential(scale=1, size=1000)
# Calcular la media (eje de simetría)
media = np.mean(data_sesgada_izquierda)
# Crear el histograma con Seaborn
plt.figure(figsize=(10, 6))
sns.histplot(data_sesgada_izquierda, bins=30, kde=True, color='blue', edgecolor='black')
# Añadir el eje de simetría
plt.axvline(media, color='red', linestyle='--', linewidth=2, label=f'Eje de Simetría (Media): {media:.2f}')
plt.title('Histograma de Datos Sesgados a la Izquierda (Asimetría Negativa)')
plt.xlabel('Valor')
plt.ylabel('Frecuencia')
plt.legend()
plt.grid(True)
plt.savefig('histograma_con_simetria.png')
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generar datos con distribución exponencial (sesgada a la derecha)
data_sesgada = np.random.exponential(scale=1, size=1000)
# Calcular la media (eje de simetría)
media = np.mean(data_sesgada)
# Crear el histograma con Seaborn
plt.figure(figsize=(10, 6))
sns.histplot(data_sesgada, bins=30, kde=True, color='green', edgecolor='black')
# Añadir el eje de simetría
plt.axvline(media, color='red', linestyle='--', linewidth=2, label=f'Eje de Simetría (Media): {media:.2f}')
plt.title('Histograma de Datos Sesgados a la Derecha (Asimetría Positiva)')
plt.xlabel('Valor')
plt.ylabel('Frecuencia')
plt.legend()
plt.grid(True)
plt.savefig('histograma_derecha_con_simetria.png')
Curtosis o apuntamiento
Es un estadístico que «indica la concentración de los valores en torno a la media, y se mide respecto a la distribución normal, que se caracteriza por ser simétrica y unimodal» (Lorente).
La expresión para hallar la curtosis es la siguiente:
$$
Curtosis = \frac{\sum_{i=1}^{N} (x_i – \bar{x})^4}{N \cdot \sigma^4} – 3
$$
Una distribución puede ser:
- Platicúrtica (menor concentración en torno a los valores centrales): $curtosis < 0$
- Mesocúrtica: $curtosis=0$
- Leptocúrtica: (mayor concentración en torno a los valores centrales): $curtosis > 0$
A continuación mostramos algunos ejemplos. Es importante tener en cuenta que hay muchos tipos de distribuciones, que pueden aplicarse para modelar fenómenos que no se distribuyen de forma «normal». Sin ir más lejos, la distribución uniforme que vimos de pasada al final de primer artículo es una distribución platicúrtica. Sin embargo, y para no perder rigurosidad, en los siguientes ejemplos usamos como base la distribución normal (que es la única que hemos analizado más o menos en profundidad hasta ahora) para ilustrar la idea.
Ejemplo de distribución platicúrtica
Una distribución platicúrtica se caracteriza por tener un pico más plano y colas más ligeras en comparación con una distribución normal. Esto significa que los datos están menos concentrados alrededor de la media y hay una menor probabilidad de valores atípicos o extremos.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import kurtosis, norm
# Set a seed for reproducibility
np.random.seed(123)
# --- Creación de una distribución Platicúrtica desde Normales ---
# 1. Generamos la primera mitad de los datos de una normal centrada a la izquierda.
# Usamos una desviación estándar más pequeña para tener colas más delgadas.
data_left = np.random.normal(loc=-1, scale=0.7, size=5000)
# 2. Generamos la segunda mitad de los datos de una normal centrada a la derecha.
data_right = np.random.normal(loc=1, scale=0.7, size=5000)
# 3. Combinamos ambos conjuntos de datos. La superposición creará una cima plana.
platykurtic_data = np.concatenate([data_left, data_right])
# Calculate the excess kurtosis (Fisher's definition, where normal = 0)
# El resultado debería ser < 0
calculated_kurtosis = kurtosis(platykurtic_data, fisher=True)
# --- Visualization ---
plt.figure(figsize=(12, 7))
# Create the plot using seaborn
sns.histplot(platykurtic_data, kde=True, bins=50, color='royalblue', stat='density', label='Distribución Empírica (Mezcla)')
# For comparison, overlay the PDF of a standard normal distribution
# Ajustamos la media y desviación de la normal de comparación a nuestros datos
# para una comparación más justa.
mean_data = np.mean(platykurtic_data)
std_data = np.std(platykurtic_data)
x_norm = np.linspace(np.min(platykurtic_data), np.max(platykurtic_data), 200)
plt.plot(x_norm, norm.pdf(x_norm, mean_data, std_data), 'r--', lw=2, alpha=0.8, label='PDF Teórica Normal (Mesocúrtica)')
# Add titles and labels
plt.title(f'Distribución Platicúrtica (Mezcla de Normales)\nCurtosis Calculada: {calculated_kurtosis:.2f}', fontsize=16)
plt.xlabel('Valor', fontsize=12)
plt.ylabel('Densidad', fontsize=12)
plt.legend()
plt.grid(True, linestyle='--', alpha=0.5)
plt.xlim(np.min(platykurtic_data), np.max(platykurtic_data)) # Adjust x-axis to fit all data
# Show the plot
plt.show()
# Print the calculated kurtosis to the console
print(f"La curtosis calculada de los datos es: {calculated_kurtosis}")
La curtosis calculada de los datos es: -0.8710986296288574
Ejemplo de distribución mesocúrtica: distribución normal
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import kurtosis, norm
# Set a seed for reproducibility
np.random.seed(202)
# Generate data from a Normal distribution (loc=mean, scale=std_dev)
# The normal distribution is the baseline for kurtosis, so it's mesokurtic.
mesokurtic_data = np.random.normal(loc=0, scale=1, size=10000)
# Calculate the excess kurtosis (Fisher's definition, where normal = 0)
# For a perfect normal distribution, this value is 0.
calculated_kurtosis = kurtosis(mesokurtic_data, fisher=True)
# --- Visualization ---
plt.figure(figsize=(12, 7))
# Create the plot using seaborn
sns.histplot(mesokurtic_data, kde=True, bins=30, color='teal', stat='density', label='Distribución Empírica')
# Overlay the theoretical probability density function (PDF) of a standard normal distribution
x = np.linspace(norm.ppf(0.001), norm.ppf(0.999), 100)
plt.plot(x, norm.pdf(x, 0, 1), 'r-', lw=2, alpha=0.8, label='PDF Teórica Normal(0,1)')
# Add titles and labels
plt.title(f'Distribución Mesocúrtica (Normal)\nCurtosis Calculada: {calculated_kurtosis:.2f}', fontsize=16)
plt.xlabel('Valor', fontsize=12)
plt.ylabel('Densidad', fontsize=12)
plt.legend()
plt.grid(True, linestyle='--', alpha=0.5)
# Show the plot
plt.show()
# Print the calculated kurtosis to the console
print(f"La curtosis calculada de los datos es: {calculated_kurtosis}")
La curtosis calculada de los datos es: 0.009464165280579806
Ejemplo de distribución leptocúrtica
Una distribución leptocúrtica se caracteriza por tener una curtosis (o apuntamiento) mayor que la de una distribución normal, lo que significa que tiene un pico más pronunciado y colas más pesadas. Esto implica que los datos están más concentrados alrededor de la media, pero también que hay una mayor probabilidad de observar valores atípicos extremos.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import kurtosis, norm
# Set a seed for reproducibility
np.random.seed(42)
# --- Creación de una distribución Leptocúrtica desde Normales ---
# 1. Generamos la mayoría de los datos (90%) de una distribución normal estándar.
data_normal_base = np.random.normal(loc=0, scale=1, size=9000)
# 2. Generamos una minoría de datos (10%) de una normal con mucha más dispersión (colas pesadas).
data_outliers = np.random.normal(loc=0, scale=5, size=1000)
# 3. Combinamos ambos conjuntos de datos.
leptokurtic_data = np.concatenate([data_normal_base, data_outliers])
# Calculate the excess kurtosis (Fisher's definition, where normal = 0)
# El resultado debería ser > 0
calculated_kurtosis = kurtosis(leptokurtic_data, fisher=True)
# --- Visualization ---
plt.figure(figsize=(12, 7))
# Create the plot using seaborn
sns.histplot(leptokurtic_data, kde=True, bins=50, color='darkred', stat='density', label='Distribución Empírica (Mezcla)')
# For comparison, overlay the PDF of a standard normal distribution
x_norm = np.linspace(norm.ppf(0.001), norm.ppf(0.999), 100)
plt.plot(x_norm, norm.pdf(x_norm, 0, 1), 'b--', lw=2, alpha=0.8, label='PDF Teórica Normal (Mesocúrtica)')
# Add titles and labels
plt.title(f'Distribución Leptocúrtica (Mezcla de Normales)\nCurtosis Calculada: {calculated_kurtosis:.2f}', fontsize=16)
plt.xlabel('Valor', fontsize=12)
plt.ylabel('Densidad', fontsize=12)
plt.legend()
plt.grid(True, linestyle='--', alpha=0.5)
plt.xlim(np.min(leptokurtic_data), np.max(leptokurtic_data)) # Adjust x-axis to fit all data
# Show the plot
plt.show()
# Print the calculated kurtosis to the console
print(f"La curtosis calculada de los datos es: {calculated_kurtosis}")
La curtosis calculada de los datos es: 12.08466019433809
Bibliografía y referencias
- Johnson, R. & Kuby, P. (2008). Estadistica elemental: lo esencial (10a ed.). Cengage Learning Editores S.A.
- Distribución normal [Internet]. Matematicasonline.es. [citado el 30 de julio de 2025]. Disponible en: https://www.matematicasonline.es/BachilleratoCCSS/segundo/archivos/distribucion_normal/DISTRIBUCION%20NORMAL.htm