Felipe Maggi.
Lenguaje de programación: Python.
- Data Science I: Población, muestra, experimentos y tipos de variables.
- Data Science II-A: Estadística descriptiva unidimensional. Tablas de frecuencia y gráficos de distribución.
- Data Science II-B: Estadística descriptiva unidimensional. Medidas de tendencia central.
- Data Science II-C: Estadística descriptiva unidimensional. Medidas de dispersión.
- Data Science II-D: Estadística descriptiva unidimensional. Medidas de posición.
- Data Science II-E: Estadística descriptiva unidimensional. La curva normal.
- Data Science III-A: Estadística descriptiva bidimensional. Dos variables cualitativas.
- Data Science III-B: Estadística descriptiva bidimensional. Una variable cualitativa y otra cuantitativa.
Los conceptos estadísticos son de dominio general, pero cuando tengamos que recurrir a una forma concreta de plantear las cosas, haremos uso, mayoritariamente, de las definiciones expuestas en el libro Estadística general: lo esencial, de Johnson & Kuby.
Conjunto de datos
Antes de continuar, vamos a recuperar el conjunto de datos simulados con los que hemos estado trabajando en toda esta serie de artículos. Recordemos que se trata de las notas de matemáticas obtenidas por alumnos de bachillerato (4 grupos, 40 alumnos por grupo, y 10 temas, lo que hace un total de 1600 notas).
import pandas as pd
import numpy as np
import random
import string
import seaborn as sns
import matplotlib.pyplot as plt
# --- CONFIGURACIÓN INICIAL ---
np.random.seed(42)
random.seed(42)
def generar_id_estudiante(n):
ids = []
for _ in range(n):
id_estudiante = ''.join(random.choices(
string.ascii_uppercase + string.digits, k=8))
ids.append(id_estudiante)
return ids
# --- PARÁMETROS ---
num_estudiantes_por_grupo = 40
total_estudiantes = num_estudiantes_por_grupo * 4
num_notas = 10
ids = generar_id_estudiante(total_estudiantes)
asignatura = 'Matemáticas'
temas = [f'Tema {i+1}' for i in range(num_notas)] # Tema 1 al 10
fecha_inicio = pd.Timestamp('2024-09-01')
grupos = ['A', 'B', 'C', 'D']
# --- FUNCIÓN para generar correlación entre notas y tiempo de estudio ---
def generar_tiempo_estudio(notas, media=270, sd_total=60, correlacion=0.75):
"""
Genera tiempos de estudio correlacionados con las notas.
"""
# 1. Calcular desviación estándar de las notas actuales
sd_notas = np.std(notas)
if sd_notas == 0: sd_notas = 1 # Evitar división por cero si todas las
# notas son iguales
# 2. Calcular la pendiente (m) necesaria
# Fórmula de regresión: m = r * (Sy / Sx)
pendiente = correlacion * (sd_total / sd_notas)
# 3. Calcular el ruido residual necesario
# Para mantener la SD total deseada, el ruido se reduce si la
# correlación es alta
sd_ruido = sd_total * np.sqrt(1 - correlacion**2)
# 4. Generar ruido y calcular tiempo
ruido = np.random.normal(0, sd_ruido, len(notas))
tiempo_estudio = media + pendiente * (notas - np.mean(notas)) + ruido
return tiempo_estudio.clip(60, 480).astype(int)
# --- GENERACIÓN DE DATOS ---
data = {
'id_estudiante': [], 'asignatura': [], 'tema': [], 'fecha': [],
'nota': [], 'calificacion': [], 'estatura': [], 'sexo': [],
'tiempo_estudio': [], 'grupo': []
}
# Asignar grupos
grupo_asignado = np.repeat(grupos, num_estudiantes_por_grupo)
random.shuffle(grupo_asignado)
for idx, id_estudiante in enumerate(ids):
fechas = [fecha_inicio + pd.DateOffset(weeks=i*4) for i in range(num_notas)]
notas = np.random.normal(6.5, 1, num_notas).clip(0, 10)
estatura = np.random.uniform(150, 190, num_notas)
sexo = random.choice(['H', 'M'])
# Usamos la nueva función (he puesto correlación 0.75 para que
# sea bien visible)
tiempo_estudio = generar_tiempo_estudio(notas, correlacion=0.75)
for i in range(num_notas):
data['id_estudiante'].append(id_estudiante)
data['asignatura'].append(asignatura)
data['tema'].append(temas[i])
data['fecha'].append(fechas[i])
data['nota'].append(round(notas[i], 2))
if 9 <= notas[i] <= 10: calificacion = 'sobresaliente'
elif 7 <= notas[i] < 9: calificacion = 'notable'
elif 5 <= notas[i] < 7: calificacion = 'aprobado'
else: calificacion = 'suspenso'
data['calificacion'].append(calificacion)
data['estatura'].append(estatura[i])
data['sexo'].append(sexo)
data['tiempo_estudio'].append(tiempo_estudio[i])
data['grupo'].append(grupo_asignado[idx])
df = pd.DataFrame(data)
df['aprobado'] = df['calificacion'].apply(lambda x: 0 if x == 'suspenso' else 1)
# Asegurar orden correcto de temas
orden_temas = [f'Tema {i}' for i in range(1, 11)]
df['tema'] = pd.Categorical(df['tema'], categories=orden_temas, ordered=True)
# Mostrar el DataFrame
print(df)
id_estudiante asignatura tema fecha nota calificacion \
0 XAJI0Y6D Matemáticas Tema 1 2024-09-01 7.00 aprobado
1 XAJI0Y6D Matemáticas Tema 2 2024-09-29 6.36 aprobado
2 XAJI0Y6D Matemáticas Tema 3 2024-10-27 7.15 notable
3 XAJI0Y6D Matemáticas Tema 4 2024-11-24 8.02 notable
4 XAJI0Y6D Matemáticas Tema 5 2024-12-22 6.27 aprobado
... ... ... ... ... ... ...
1595 FNKOMV2X Matemáticas Tema 6 2025-01-19 4.28 suspenso
1596 FNKOMV2X Matemáticas Tema 7 2025-02-16 7.87 notable
1597 FNKOMV2X Matemáticas Tema 8 2025-03-16 5.41 aprobado
1598 FNKOMV2X Matemáticas Tema 9 2025-04-13 7.76 notable
1599 FNKOMV2X Matemáticas Tema 10 2025-05-11 7.45 notable
estatura sexo tiempo_estudio grupo aprobado
0 157.272999 H 331 C 1
1 157.336180 H 222 C 1
2 162.169690 H 285 C 1
3 170.990257 H 283 C 1
4 167.277801 H 203 C 1
... ... ... ... ... ...
1595 173.907293 M 180 A 0
1596 184.787835 M 310 A 1
1597 185.633286 M 253 A 1
1598 167.961510 M 266 A 1
1599 168.372148 M 317 A 1
[1600 rows x 11 columns]
Datos bivariados
Nuestros autores de referencia definen los datos bivariados como
«los valores de dos variables diferentes, que se obtienen del mismo elemento poblacional» (Johnson & Kuby).
Los mismos autores explican que «cada una de las dos variables puede ser cualitativa o cuantitativa. En consecuencia, tres combinaciones de tipos de variables pueden formar datos bivariados:
- Ambas variables son cualitativas.
- Una variable es cualitativa y la otra es cuantitativa.
- Ambas variables son cuantitativas» (el caso que ahora nos ocupa).
Según Johnson & Kuby
«Cuando se trabaja con dos variables cuantitativas se acostumbra a expresar los datos como pares ordenados $(x,y)$, donde $x$ es la variable de entrada (a veces llamada variable independiente) e $y$ es la variable de salida (a veces llamada variable dependiente). Se dice que los datos están ordenados porque el valor $x$ siempre se escribe primero«.
Supongamos que cuando se realiza un examen de matemáticas, los profesores preguntan a cada alumno cuánto tiempo ha estudiado para ese examen, y lo registran en una base de datos (en minutos). Por lo tanto, para cada tiempo de estudio (la variable $x$, o independiente), tenemos relacionada una nota concreta (la variable $y$, o dependiente). La siguiente tabla muestra los primeros 10 pares ordenados de tiempo de estudio y notas:
df_display = df[['tiempo_estudio', 'nota']].head(10)
display(df_display)
| tiempo_estudio | nota | |
|---|---|---|
| 0 | 331 | 7.00 |
| 1 | 222 | 6.36 |
| 2 | 285 | 7.15 |
| 3 | 283 | 8.02 |
| 4 | 203 | 6.27 |
| 5 | 229 | 6.27 |
| 6 | 298 | 8.08 |
| 7 | 305 | 7.27 |
| 8 | 185 | 6.03 |
| 9 | 264 | 7.04 |
La forma más rápida y sencilla de «ver» esto es mediante un diagrama de dispersión, un tipo de gráfico que suele usarse siempre que se opera con dos variables cuantitativas, y en el que «todos los pares ordenados de datos se representan en un sistema de ejes de coordenadas. La variable de entrada (o independiente), $x$, se localiza en el eje horizontal, y la variable de salida (o dependiente), $y$, se localiza en el eje vertical» (Johnson & Kuby).
El siguiente gráfico muestra la dispersión entre notas y tiempo de estudio:
import seaborn as sns
import matplotlib.pyplot as plt
# 1. Configurar el tamaño del gráfico
plt.figure(figsize=(10, 6))
# 2. Crear el Scatterplot
# data: tu dataframe
# x: eje horizontal (variable independiente)
# y: eje vertical (variable dependiente)
# alpha=0.5: Transparencia (0 a 1) para ver mejor si hay puntos superpuestos
# s=50: Tamaño de los puntos
sns.scatterplot(data=df, x='tiempo_estudio', y='nota', alpha=0.5, s=50)
<Axes: xlabel='tiempo_estudio', ylabel='nota'>
Si observamos el diagrama con detenimiento, vemos que hay casos en los que mayores tiempos de estudio han dado como resultado notas más bajas y viceversa. Esto es así porque el tiempo de estudio no explica, por sí solo, la nota obtenida. Hay otros factores que también influyen, que aquí no se han tenido en cuenta, como puede ser la capacidad innata de una persona en temas relacionados con las matemáticas, o su nivel socioeconómico. Pero no nos adelantemos.
Correlación lineal
Tomando como base las explicaciones de Johnson & Kuby, podemos decir que el análisis de correlación lineal mide el sentido y la fuerza de la relación entre las dos variables estudiadas (en este caso, tiempo de estudio y notas obtenidas).
En términos simples, se puede decir que existe correlación lineal si el diagrama de dispersión nuestra una nube de puntos con forma de elipse, que no es paralela a ninguno de los ejes, sobre la que se puede trazar una recta que no se sale de dicha nube de puntos (es importante tener en cuenta que la ventana de visualización, o dicho de otro modo, las escalas de los ejes $x$ e $y$, influyen en la forma de la nube de puntos, por lo que debemos asegurarnos de tener una ventana más o menos cuadrada).
El sentido de la relación, sin entrar en detalles matemáticos, puede explicarse de la siguiente manera:
- Si cuando aumenta $x$ aumenta $y$, la correlación es positiva.
- Si cuando $x$ aumenta $y$ disminuye, la correlación es negativa.
Por otra parte, si un cambio en $x$ no produce en cambio definido en $y$, significa que no hay correlación entre las variables.
El caso del tiempo de estudio y las notas es un ejemplo de correlación positiva. Un ejemplo de correlación negativa podría ser la relación entre los caballos de potencia de un motor, y el número de kilómetros recorridos por cada litro de combustible. A más caballos de potencia, menos distancia.
La correlación puede ser más o menos fuerte. Cuando la correlación es alta, la nube de puntos es estrecha y se asemeja más a una línea recta.
Los gráficos siguientes ilustran estos conceptos:
Dos variables pueden estar relacionadas, aunque dicha relación no sea lineal. En ese caso no hay correlación lineal. Los siguientes gráficos son un ejemplo de esto último:
Covarianza
Ahora intentaremos dar algo de rigor matemático al tema, empezando por definir la covarianza.
La covarianza es una medida estadística que nos indica el sentido de la relación entre las variables de estudio. Su fórmula matemática es:
$$
Cov(X, Y) = \frac{\sum (x_i – \bar{x})(y_i – \bar{y})}{n}
$$
donde:
- $x_i$ es el valor i-ésimo de que toma la variable $x$.
- $y_i$ es es el valor i-ésimo que toma la variable $y$ (que se corresponde con el con el valor i-ésimo de la variable $x$).
- $\bar{x}$ es la media de los valores de $x$.
- $\bar{y}$ es la media de las los valores de $y$.
- $n$ es el tamaño de la muestra (si trabajamos con toda la población sería $N$).
Puesta en palabras, es el promedio de los productos de las desviaciones de cada par de datos respecto a su media. Nos indica si, «en promedio», cuando $x$ se aleja de su centro, $y$ también lo hace y en qué sentido.
La covarianza determina el signo de la correlación, y puede ser:
- Positiva ($>0$): en promedio, cuando aumenta $x$ aumenta $y$.
- Negativa ($<0$): en promedio, cuando aumenta $x$ disminuye $y$.
- Covarianza Cercana a Cero ($\approx 0$): Indica que no hay una relación lineal clara entre las dos variables.
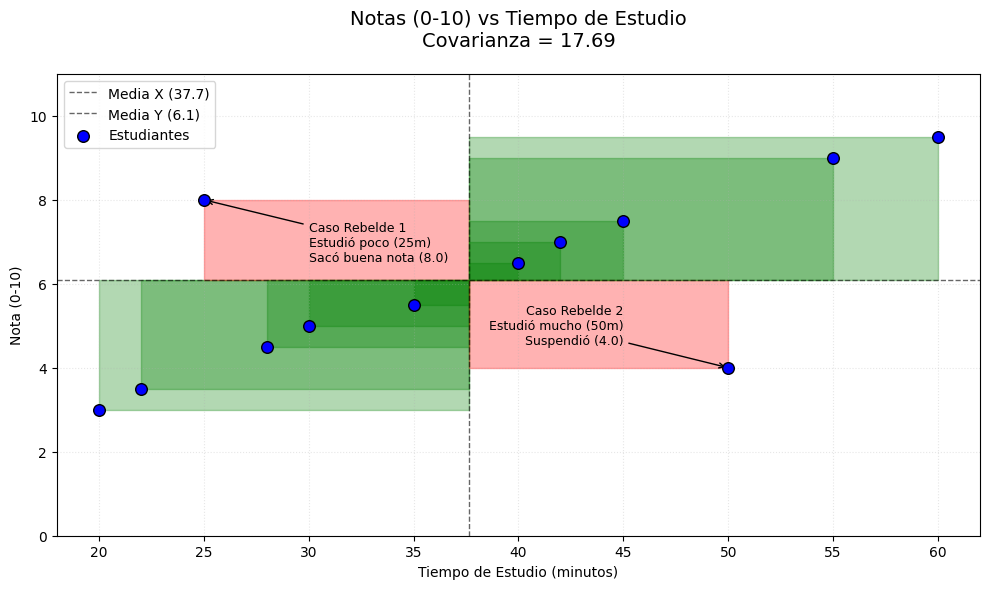
Para explicarlo mejor, vamos a visualizarlo. Supongamos que tenemos una muestra de tiempos de estudio y notas, y que esa muestra es la siguiente:
- Tiempo de estudio ($\bar{x}$): 37,67 minutos
- Nota ($\bar{y}$): 6,08
De la muestra cogemos, por ejemplo, la segunda línea de la tabla:
- Tiempo de estudio ($x_2$): 22,00 minutos
- Nota ($y_2$): 3,50
En este caso concreto, la expresión sería:
$$
(x_2 – \bar{x})(y_2 – \bar{y}) = (22,00 – 37,67)(3,50-6,08)=(-15,67)(-2,58)=40,43
$$
Si nos fijamos bien, al multiplicar $(−15,67)(−2,58)$ lo que obtenemos es un área de ancho -15,67 (que es la distancia que hay entre 22,00 y 37,67) por alto -2,58 (que es la distancia que hay entre 3,50 y 6,08). Como ambos términos son negativos, el area es positiva.
Si ahora hacemos lo mismo con la décima línea, los datos son:
- Tiempo de estudio ($x_{10}$): 50,00 minutos
- Nota ($y_{10}$): 4,00
Tenemos:
$$
(x_{10} – \bar{x})(y_{10} – \bar{y}) = (50,00 – 37,67)(4,00-6,08)=(12,33)(-2,08)=-25,65
$$
En este caso, el alumno ha estudiado 12,33 minutos por encima de la media del tiempo de estudio, pero ha sacado un 4,00, es decir, 2,08 puntos por debajo de la nota media. Como la primera cantidad es positiva, y la segunda negativa, el área es negativa:
Veamos ahora el caso de la última observación (línea 12):
- Tiempo de estudio ($x_{12}$): 60,00 minutos
- Nota ($y_{12}$): 9,50
Los cálculos son:
$$
(x_{12} – \bar{x})(y_{12} – \bar{y}) = (60,00 – 37,67)(9,50-6,08)=(22,33)(3,42)=76,37
$$
En este caso, ambas magnitudes son positivas, por lo que el área es positiva:
Si repetimos esta operación para todas las observaciones de la muestra, obtendremos todas las áreas correspondientes:
Al sumar todas las áreas y dividirlas por el tamaño de la muestra, estamos obteniendo el área media que es, precisamente, la covarianza.
Que la covarianza sea positiva significa que el valor absoluto de la suma de las áreas verdes es mayor que el de la suma de las áreas rojas, por lo que numerador de la fórmula es positivo. La visualización muestra claramente que, en ese caso, cuando $x$ aumenta, $y$, en promedio, también lo hace.
La expresión «en promedio» se debe a que, aunque la tendencia sea esa (si aumenta $x$, aumenta $y$), puede haber casos en los que eso no ocurra, como hemos visto en este ejemplo, donde hay dos casos en los que la tendencia general no se cumple.
Si la covarianza es negativa, la pendiente de los puntos se invierte, y el valor absoluto de la suma de las areas verdes es menor que el valor absoluto de la suma de las areas rojas. Como ejemplo podríamos poner las horas que el estudiante dedica a los videojuegos, y las notas de matemáticas. A más horas jugando con la consola, menos horas de estudio, y de sueño. Es lógico pensar que, en promedio, mientras más se juega, menos nota se obtiene:
Nos queda aún el caso de la varianza nula, o cercana a cero.
Supongamos que la lógica nos ha fallado, y que cuando observamos el gráfico de dispersión entre horas diarias de videojuegos y notas vemos que no hay un patrón definido.
El siguiente gráfico muestra claramente porqué cuando un gráfico de dispersión no muestra un patrón definido significa que la covarianza es cercana a cero:
Las areas verdes, que suman porque son positivas, y las rojas, que restan porque son negativas, se cancelan entre sí cuando se realiza el sumatorio. El valor de numerador es pequeño, y al dividirlo por el tamaño de la muestra se hace más pequeño aún. No se puede decir que, en promedio, $y$ crezca o decrezca cuando $x$ crece o decrece.
Coeficiente de correlación lineal ($r$)
Ahora que entendemos el concepto de covarianza, podemos adentrarnos en el de coeficiente de correlación lineal.
Aunque la covarianza nos dice dice si la relación entre las variables es positiva o negativa, no nos sirve para valorar la «fuerza» de esa relación, ni para comparar esa fuerza entre distintos casos. Esto se debe a que la covarianza depende de las unidades de medida. Si las unidades son grandes, las magnitudes absolutas de las áreas también lo son, y viceversa.
Para solucionar esto, y medir la fuerza de la relación sin que las unidades de los datos no afecten, podemos utilizar el coeficiente de correlación lineal de Pearson ($r$).
El coeficiente de correlación lineal de Pearson normaliza la covarianza, que acabamos de definir, al dividirla por el producto entre las desviaciones estándar de $x$ e $y$:
$$
r = \frac{Cov(X, Y)}{\sigma_x \cdot \sigma_y}
$$
Si la desarrollamos, la fórmula es:
$$r = \frac{\sum (x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum (x_i – \bar{x})^2} \cdot \sqrt{\sum (y_i – \bar{y})^2}}$$
Viendo la expresión, puede resultar complicado entender por qué soluciona el problema de las unidades de medida, y por qué es capaz de cuantificar la fuerza de la relación lineal. Vamos primero a intentar explicar el problema de las unidades.
Cancelación de unidades
Imaginemos que una persona de España, quiere comprar una casa en Santiago de Chile. Para estimar más o menos el precio que tendrá que pagar, se informa y descubre que, en el barrio de su interés, una casa cuesta, de media, unos 3 millones de pesos Chilenos (CLP) por metro cuadrado construido (m²). Las unidades de esta magnitud son CLP/m².
En ese barrio, el precio medio de las casas es de 240 millones CLP, y el tamaño medio es de 80 m².
Navega por internet, y encuentra una casa que le gusta. La casa cuesta 270 millones y tiene 100 metros cuadrados. Es decir, esa casa en concreto tiene un precio que está 30 millones CLP por encima de la media de precio, y tiene 20 m² más que la media de superficie construida.
El numerador
Si en el eje $x$ tenemos metros cuadrados, y en el eje $y$ millones de pesos, el área que representa a esa casa en concreto en los gráficos de covarianza que hemos visto antes es de 600 millones, y sus unidades son m² * CLP (no hay que intentar buscarle el sentido a esas unidades).
20m² por encima de la media * 30 millones CLP por encima de la media = 600 millones m² * CLP
Pero claro, esa persona de España querrá pasar los cálculos a Euros (EUR), así que se pone manos a la obra. Busca de nuevo en internet y descubre que 1 euro equivale aproximadamente, al cambio del día, a 1.068 pesos chilenos. Si hacemos las conversiones necesarias, los datos quedan, aproximadamente, así:
- Precio del metro cuadrado: 2.809 EUR
- Precio de la casa: 252.809 EUR
- Precio medio de las casas 224.719 EUR
- Los metros cuadrados son los mismos.
Por lo tanto, el area que forma la casa en concreto ahora tiene una magnitud aproximada de 561.800 m² * EUR:
28.090 EUR por encima de la media * 20m² por encima de la media = 561.800 m² * EUR
En ambos casos el área es positiva, y probablemente si tuviéramos más datos comprobaríamos que las areas positivas suman más que las negativas (a más metros cuadrados, más caras son las casas). La covarianza será positiva tanto si trabajamos en pesos chilenos como en euros, pero estará en el orden de decenas de millones en el primer caso, y de cientos de miles, en el segundo, sin que eso signifique la fuerza de la relación sea distinta (más fuerte en el caso de los pesos). Es evidente que la relación es la misma. Sólo hemos cambiado la escala de los números, no la naturaleza de la relación entre las variables.
El denominador
$$ \frac{1}{n}\sqrt{\sum (x_i – \bar{x})^2} \cdot \sqrt{\sum (y_i – \bar{y})^2}$$
En el denominador tenemos una expresión más compleja. A los sumatorios hay que añadir expresiones elevadas al cuadrado, y raíces cuadradas. Pero basta con recordar que exponentes y raíces se cancelan entre sí:
$$\sqrt{2^2} = 2$$
El denominador no otra cosa que la desviación estándar de $x$, multiplicada por la desviación estándar de $y$. Como sabemos, la desviación estándar de una cantidad está en las mismas unidades que dicha cantidad (recomendamos repasar el artículo en el que tratamos las medidas de dispersión, entre ellas la desviación estándar).
Nota: el término $\frac{1}{n}$ se cancela, porque está presente tanto en el numerador como en el denominador.
Digamos que la desviación estándar de la superficie construida es de 30m² y, en el caso de los pesos chilenos, la desviación estándar del precio de las casas es de 20 millones CLP. Por lo tanto, en el denominador también tendremos las unidades m² * CLP, y éstas se cancelan. Si trabajamos en euros pasa lo mismo.
$$ \frac{ \rlap{\rule[3.5pt]{4.6em}{0.5pt}} m^2 \cdot \text{CLP} }{ \rlap{\rule[3.5pt]{4.6em}{0.5pt}} m^2 \cdot \text{CLP} } $$
Recurriremos a las razones y a las proporciones para visualizar esto con más detalle.
Supongamos que la persona interesada en la casa, quiere saber cuánto más grande es la casa que ha visto con respecto a la media. Si divide 100m² entre 80m² obtiene 1,25 lo que equivale al 125 por ciento. Es decir, es un 25% más grande que la media.
Luego se pregunta cuánto más cara es la casa con respecto a la media de precios en ese barrio, así que repite la operación con pesos chilenos:
$$ \frac{270.000.000 \, \rlap{\rule[3.5pt]{2.1em}{0.5pt}} \text{CLP} }{ 240.000.000 \, \rlap{\rule[3.5pt]{2.1em}{0.5pt}} \text{CLP} } = 1,125 $$
Resulta que la casa es un 25% más grande que la media, pero sólo casi un 13% más cara. Parece que el precio es más que justo. Pero no se queda tranquilo y lo calcula otra vez, en euros:
$$ \frac{252.809 \, \rlap{\rule[3.5pt]{2.1em}{0.5pt}} \text{EUR} }{224.719 \, \rlap{\rule[3.5pt]{2.1em}{0.5pt}} \text{EUR} } = 1,125 $$
Los resultados son iguales, y las conclusiones también. Evidentemente, la explicación matemática por la que ambos resultados son iguales es que 270 millones son equivalentes, al cambio, a 252.809 euros, y 240 millones de pesos son equivalentes a 224.719 euros. Ambas razones son proporcionales, y la constante de proporcionalidad es 1.068 pesos por euro.
$$ \frac{270.000.000 \, \rlap{\rule[3.5pt]{2.1em}{0.5pt}} \text{CLP} }{ 240.000.000 \, \rlap{\rule[3.5pt]{2.1em}{0.5pt}} \text{CLP} } = \frac{252.809 \, \rlap{\rule[3.5pt]{2.1em}{0.5pt}} \text{EUR} * \rlap{\rule[3.5pt]{2.5em}{0.5pt}} 1.068 \, \rlap{\rule[3.5pt]{4.8em}{0.5pt}} \text{CLP/EUR} }{224.719 \, \rlap{\rule[3.5pt]{2.1em}{0.5pt}} \text{EUR} * \rlap{\rule[3.5pt]{2.5em}{0.5pt}} 1.068 \, \rlap{\rule[3.5pt]{4.8em}{0.5pt}} \text{CLP/EUR} } = 1,125 $$
Una razón es una magnitud abstracta adimensional, de la misma forma en que lo es el coeficiente de correlación lineal ($r$), que no depende en absoluto de la escala o las unidades de las variables, puesto que éstas se cancelan en la operativa.
Las notas y los tiempos de estudio
En el caso de las notas, pasa lo mismo. Si la unidad del tiempo de estudio son los minutos, y la de las notas son los «puntos» (una nota puede ir de cero a diez puntos, o de cero a 100, dependiendo de la escala), tanto en el numerador como en el denominador tenemos:
$$ \frac{ \rlap{\rule[3.5pt]{8.8em}{0.5pt}} minutos \cdot \text{puntos} }{ \rlap{\rule[3.5pt]{8.8em}{0.5pt}} minutos \cdot \text{puntos} } $$
La fuerza de la relación
Ahora nos queda intentar explicar por qué el coeficiente de correlación lineal de Pearson nos indica la fuerza de la relación.
Como hemos adelantado antes, $r$ es una razón, y una razón es una comparación entre dos números que se lee $a$ es a $b$:
$$
\frac{a}{b}
$$
En el numerador (en términos de razones se denomina antecedente) tenemos la covarianza que, como ya sabemos, es la suma de todas las áreas que forman los puntos de datos (cuyo ancho es la distancia del punto a la media del eje $x$, y cuyo alto es la distancia del mismo punto a la media del eje $y$), dividida por el tamaño de la muestra. En otras palabras, es el área media que conforman todos esos puntos tomando como referencia los valores medios de cada variable.
En el denominador (el consecuente) tenemos otra área: la que forma la desviación estándar de $x$ multiplicada por la desviación estándar de $y$, y ya sabemos que la desviación estándar de una variable siempre será positiva (porque se obtiene elevando las diferencias al cuadrado). El denominador siempre será mayor o igual numerador (la covarianza), puesto que la covarianza se calcula con el sumatorio de areas positivas (que suman) y negativas (que restan), mientras que en el denominador no hay términos negativos.
En definitiva, estamos comparando la magnitud de un área, con la magnitud de otra.
Si los puntos de datos forman en el gráfico de dispersión una línea recta perfecta, el valor absoluto del numerador es el mismo que el del denominador. Por lo tanto, $r$ puede tomar un rango de valores específico que va de -1 (cuando la correlación es negativa perfecta) a +1 (cuando la correlación es positiva perfecta). En términos matemáticos:
$$
-1 \leq r \leq +1
$$
Al final de este artículo se explica algebraicamente porqué cuando la correlación es perfecta $r$ es $-1$ o $1$.
Como haya un solo punto que se salga de la recta, el valor absoluto del numerador será menor que el valor absoluto del denominador. Mientras más puntos se salgan de la recta, más pequeño (en términos absolutos) será el numerador con respecto al denominador. El siguiente gráfico permite observar esto:
La covarianza de la muestra de 12 notas es $17,69$, y el área que forman las desviaciones estándar de $x$ e $y$ es $29,09$. La correlación $r$ es:
$$
\frac{17,69}{26,09} = 0,678
$$
En palabras:
- $17,69$ es a $26,09$ el $0,678$
o, más claro aún:
- $17,69$ es el $67,8\%$ de $26,09$.
La «fuerza» de la relación es el $67,8\%$ del máximo posible.
Cuando el numerador es cero o cercano a cero, $r$ también es cero o cercano a cero, y eso ocurre, como hemos visto, cuando los puntos no forman un patrón definido.
Volvamos a nuestro diagrama de dispersión original, con los 1600 puntos que representan los tiempos de estudio y las notas de nuestro conjunto de datos base, y añadamos la función para el cáculo de la correlación entre ambas variables:
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
sns.scatterplot(data=df, x='tiempo_estudio', y='nota', alpha=0.5, s=50)
correlacion_real = df['tiempo_estudio'].corr(df['nota'])
plt.title(f'Validación: Tiempo de Estudio vs Nota')
plt.xlabel('Tiempo de Estudio (minutos)')
plt.ylabel('Nota')
plt.grid(True, linestyle='--', alpha=0.6)
plt.show()
correlacion = df['tiempo_estudio'].corr(df['nota'])
print(correlacion)
0.7039324480703348
- 0: correlación nula
- 0,10 – 0,29: correlación débil
- 0,30 – 0,49: correlación moderada
- 0,50 – 0,69: correlación fuerte
- 0,70 – 0,89: correlación muy fuerte
- 0,90 – 1,00: correlación perfecta
Es necesario recordar que debemos fijarnos en los valores absolutos. Una correlación de -0,75 es también una correlación muy fuerte, pero negativa.
Correlación no implica causalidad
Que dos variables numéricas estén relacionadas no significa que una sea causa de la otra. En el caso de notas y los tiempos de estudio quizá es posible argumentar que una nota determinada es, en parte, la causa del tiempo de estudio dedicado. Pero esto no tiene porqué ser así siempre. Hay casos en los que dos variables tienen una fuerte correlación que en realidad se debe a una tercera variable. El ejemplo más común es el número de helados vendidos y el número de ahogamientos acaecidos en un balneario y período concretos: a más helados vendidos, más ahogamientos.
Evidentemente, «los helados no causan ahogamientos, sino que la gente come más helados en los días calurosos, cuando también es más probable que vayan a nadar» (otexts.com).
Hay en Internet una página con correlaciones espúrias muy graciosas, que vale la pena consultar: https://www.tylervigen.com/spurious-correlations. Algunas de ellas son lineales y otras no, pero todas ilustran perfectamente el hecho de que la correlación no implica causalidad.
La explicación algebraica de lo que pasa cuando la correlación es perfecta
Como se demuestra a partir de la Desigualdad de Cauchy-Schwarz aplicada a la covarianza (ver Walpole et al. o DeGroot), cuando existe una relación lineal exacta $Y = a + bX$, el coeficiente de correlación de Pearson es igual a $\pm 1$.
Si la correlación es perfecta, los puntos caen exactamente en una línea recta. Cuando $x$ se mueve una distancia, $y$ se mueve esa misma distancia multiplicada por un número fijo ($k$). En términos matemáticos:
- La parte de $x$ queda igual: $\sqrt{\sum (x_i – \bar{x})^2}$
- La parte de $y$ podemos sustituirla por $$ \sqrt{\sum (k \cdot (x_{i}-\bar{x}))^2} = \sqrt{k^2 \sum (x_{i}-\bar{x})^2} = |k| \sqrt{\sum (x_{i}-\bar{x})^2} $$
Si multiplicamos ambar partes:
$$\sqrt{\sum (x_i – \bar{x})^2} \cdot |k| \sqrt{\sum (x_{i}-\bar{x})^2} = |k| \sum (x_i-\bar{x})^2 $$
La expresión final de $r$, tras estas sustituciones, queda así:
- Si $k$ es positivo, el resultado es $1$
- Si $k$ es negativo, el resultado es $-1$
Spoiler
Hemos llegado, con este artículo, a un punto de inflexión. Hasta ahora se han tratado temas relacionados con el análisis descriptivo de los datos. En la siguiente entrega abordaremos la regresión lineal, que es quizá el primer y más básico método de estimación del valor de una variable, a partir del valor de otra.
Bibliografía y referencias
- Johnson, R. & Kuby, P. Estadística elemental: lo esencial (10a ed.). Cengage Learning Editores S.A. (2008).
- 7.8 Correlación, causalidad y predicción [Internet]. Otexts.com. [citado 9 de enero de 2026]. Disponible en: https://otexts.com/fppsp/causalidad.html
- Spurious correlations [Internet]. Tylervigen.com. [citado 9 de enero de 2026]. Disponible en: https://www.tylervigen.com/spurious-correlations
- Para encontrar una forma visual de explicar la covarianza, y para enfocar la explicación algebraica del caso de correlación perfecta, hemos hecho uso de Gemini Pro 3.0. La explicación algebraica de Gemini, a su vez, se basa en varias fuentes. La más directa es Walpole, R. E., Myers, R. H., et al. «Probabilidad y estadística para ingeniería y ciencias». Sin embargo, la razón profunda por la que el numerador es menor o igual al denominador (y solo igual cuando son proporcionales) se basa en la Desigualdad de Cauchy-Schwarz, que se trata en libros como «Statistical Inference» de Casella & Berger o «Probability and Statistics» de DeGroot & Schervish. Otras fuentes usadas por Gemini para esta cuestión son:
- David S. Moore, «Estadística básica» (The Basic Practice of Statistics)
- Ken Black, «Estadística para los negocios» (Business Statistics)
Artículo siguiente: Dos Variables cualitativas. Regresión Lineal —>
Artículo anterior: <— Una variable cualitativa y otra cuantitativa