Felipe Maggi.
Lenguaje de programación: Python.
La cuestión es: ¿si vemos que hay cierta correlación entre las variables, calculamos el coeficiente de correlación lineal de Pearson y obtenemos un valor que puede considerarse como «fuerte» o «muy fuerte», no tendrá sentido encontrar una función que genere una recta que se ajuste lo más posible a la nube de puntos, y que nos permita estimar, más o menos, el valor de la variable dependiente a partir de la variable independiente?
En esta serie de artículos dedicados a la Ciencia de Datos, ya hemos publicado los capítulos:
- Data Science I: Población, muestra, experimentos y tipos de variables.
- Data Science II-A: Estadística descriptiva unidimensional. Tablas de frecuencia y gráficos de distribución.
- Data Science II-B: Estadística descriptiva unidimensional. Medidas de tendencia central.
- Data Science II-C: Estadística descriptiva unidimensional. Medidas de dispersión.
- Data Science II-D: Estadística descriptiva unidimensional. Medidas de posición.
- Data Science II-E: Estadística descriptiva unidimensional. La curva nornal.
- Data Science III-A: Estadística descriptiva bidimensional. Dos variables cualitativas.
- Data Science III-B: Estadística descriptiva bidimensional. Una variable cualitativa y otra cuantitativa.
- Data Science III-C: Estadística descriptiva bidimensional. Dos variables cuantitativas. Correlación Lineal.
Para cada uno de estos temas hay mucha bibliografía disponible, y nos hemos guiado, en parte, por lo expuesto en el material del Máster de Big Data & Data Science de la Universidad de Barcelona, en concreto por Dolores Lorente.
Los conceptos estadísticos son de dominio general, pero cuando tengamos que recurrir a una forma concreta de plantear las cosas, haremos uso, mayoritariamente, de las definiciones expuestas en el libro Estadística general: lo esencial, de Johnson & Kuby.
En el artículo anterior repasamos la correlación lineal con bastante detalle, empezando por una definición informal y terminando con una explicación algebraica del porqué puede tomar valores de -1 o 1 cuando la correlación es perfecta. En el camino de un punto a otro, definimos la covarianza apoyándonos en gráficos y vimos por qué el coeficiente de correlación lineal de Pearson es una métrica adimensional capaz de cuantificar la fuerza de una relación entre variables.
Llegados a este punto, el siguiente paso lógico es intentar estimar el valor de una variable (la variable dependiente) a partir del valor de otra (la variable independiente). Eso es precisamente lo que se pretende con la regresión lineal, pero vayamos por partes.
Conjunto de datos
Antes de continuar, vamos a recuperar el conjunto de datos simulados con los que hemos estado trabajando en toda esta serie de artículos. Recordemos que se trata de las notas de matemáticas obtenidas por alumnos de bachillerato (4 grupos, 40 alumnos por grupo, y 10 temas, lo que hace un total de 1600 notas).
import pandas as pd
import numpy as np
import random
import string
import seaborn as sns
import matplotlib.pyplot as plt
# --- CONFIGURACIÓN INICIAL ---
np.random.seed(42)
random.seed(42)
def generar_id_estudiante(n):
ids = []
for _ in range(n):
id_estudiante = ''.join(random.choices(
string.ascii_uppercase + string.digits, k=8))
ids.append(id_estudiante)
return ids
# --- PARÁMETROS ---
num_estudiantes_por_grupo = 40
total_estudiantes = num_estudiantes_por_grupo * 4
num_notas = 10
ids = generar_id_estudiante(total_estudiantes)
asignatura = 'Matemáticas'
temas = [f'Tema {i+1}' for i in range(num_notas)] # Tema 1 al 10
fecha_inicio = pd.Timestamp('2024-09-01')
grupos = ['A', 'B', 'C', 'D']
# --- FUNCIÓN para generar correlación entre notas y tiempo de estudio ---
def generar_tiempo_estudio(notas, media=270, sd_total=60, correlacion=0.75):
"""
Genera tiempos de estudio correlacionados con las notas.
"""
# 1. Calcular desviación estándar de las notas actuales
sd_notas = np.std(notas)
if sd_notas == 0: sd_notas = 1 # Evitar división por cero si todas las
# notas son iguales
# 2. Calcular la pendiente (m) necesaria
# Fórmula de regresión: m = r * (Sy / Sx)
pendiente = correlacion * (sd_total / sd_notas)
# 3. Calcular el ruido residual necesario
# Para mantener la SD total deseada, el ruido se reduce si la
# correlación es alta
sd_ruido = sd_total * np.sqrt(1 - correlacion**2)
# 4. Generar ruido y calcular tiempo
ruido = np.random.normal(0, sd_ruido, len(notas))
tiempo_estudio = media + pendiente * (notas - np.mean(notas)) + ruido
return tiempo_estudio.clip(60, 480).astype(int)
# --- GENERACIÓN DE DATOS ---
data = {
'id_estudiante': [], 'asignatura': [], 'tema': [], 'fecha': [],
'nota': [], 'calificacion': [], 'estatura': [], 'sexo': [],
'tiempo_estudio': [], 'grupo': []
}
# Asignar grupos
grupo_asignado = np.repeat(grupos, num_estudiantes_por_grupo)
random.shuffle(grupo_asignado)
for idx, id_estudiante in enumerate(ids):
fechas = [fecha_inicio + pd.DateOffset(weeks=i*4) for i in range(num_notas)]
notas = np.random.normal(6.5, 1, num_notas).clip(0, 10)
estatura = np.random.uniform(150, 190, num_notas)
sexo = random.choice(['H', 'M'])
# Usamos la nueva función (he puesto correlación 0.75 para que
# sea bien visible)
tiempo_estudio = generar_tiempo_estudio(notas, correlacion=0.75)
for i in range(num_notas):
data['id_estudiante'].append(id_estudiante)
data['asignatura'].append(asignatura)
data['tema'].append(temas[i])
data['fecha'].append(fechas[i])
data['nota'].append(round(notas[i], 2))
if 9 <= notas[i] <= 10: calificacion = 'sobresaliente'
elif 7 <= notas[i] < 9: calificacion = 'notable'
elif 5 <= notas[i] < 7: calificacion = 'aprobado'
else: calificacion = 'suspenso'
data['calificacion'].append(calificacion)
data['estatura'].append(estatura[i])
data['sexo'].append(sexo)
data['tiempo_estudio'].append(tiempo_estudio[i])
data['grupo'].append(grupo_asignado[idx])
df = pd.DataFrame(data)
df['aprobado'] = df['calificacion'].apply(lambda x: 0 if x == 'suspenso' else 1)
# Asegurar orden correcto de temas
orden_temas = [f'Tema {i}' for i in range(1, 11)]
df['tema'] = pd.Categorical(df['tema'], categories=orden_temas, ordered=True)
# Mostrar el DataFrame
print(df)
id_estudiante asignatura tema fecha nota calificacion \
0 XAJI0Y6D Matemáticas Tema 1 2024-09-01 7.00 aprobado
1 XAJI0Y6D Matemáticas Tema 2 2024-09-29 6.36 aprobado
2 XAJI0Y6D Matemáticas Tema 3 2024-10-27 7.15 notable
3 XAJI0Y6D Matemáticas Tema 4 2024-11-24 8.02 notable
4 XAJI0Y6D Matemáticas Tema 5 2024-12-22 6.27 aprobado
... ... ... ... ... ... ...
1595 FNKOMV2X Matemáticas Tema 6 2025-01-19 4.28 suspenso
1596 FNKOMV2X Matemáticas Tema 7 2025-02-16 7.87 notable
1597 FNKOMV2X Matemáticas Tema 8 2025-03-16 5.41 aprobado
1598 FNKOMV2X Matemáticas Tema 9 2025-04-13 7.76 notable
1599 FNKOMV2X Matemáticas Tema 10 2025-05-11 7.45 notable
estatura sexo tiempo_estudio grupo aprobado
0 157.272999 H 331 C 1
1 157.336180 H 222 C 1
2 162.169690 H 285 C 1
3 170.990257 H 283 C 1
4 167.277801 H 203 C 1
... ... ... ... ... ...
1595 173.907293 M 180 A 0
1596 184.787835 M 310 A 1
1597 185.633286 M 253 A 1
1598 167.961510 M 266 A 1
1599 168.372148 M 317 A 1
[1600 rows x 11 columns]
Diagrama de dispersión
El siguiente gráfico nos muestra el diagrama de dispersión entre notas y tiempo de estudio, que ya vimos en el artículo precedente:
La cuestión es: ¿si vemos que hay cierta correlación entre las variables, calculamos el coeficiente de correlación lineal de Pearson y obtenemos un valor que puede considerarse como «fuerte» o «muy fuerte», no tendrá sentido encontrar una función que genere una recta que se ajuste lo más posible a la nube de puntos, y que nos permita estimar, más o menos, el valor de la variable dependiente a partir de la variable independiente?
No es casualidad que en el artículo anterior hayamos definido de manera informal la correlación lineal diciendo que esta existe cuando «el diagrama de dispersión nuestra una nube que no es paralela a ninguno de los ejes, sobre la que se puede trazar una recta que no se sale de dicha nube de puntos«.
El coeficiente de correlación lineal entre las notas y el tiempo de estudio es de 0,7039 (70,4%), tal y como se puede comprobar con la función correspondiente de Python:
correlacion = df['tiempo_estudio'].corr(df['nota'])
print(correlacion)
0.7039324480703348
Es una correlación muy fuerte, si nos guiamos por esta tabla de referencia (no existe una tabla única, y según la fuente la clasificación puede variar ligeramente, pero es válida a los efectos de este artículo):
- 0: correlación nula
- 0,10 – 0,29: correlación débil
- 0,30 – 0,49: correlación moderada
- 0,50 – 0,69: correlación fuerte
- 0,70 – 0,89: correlación muy fuerte
- 0,90 – 1,00: correlación perfecta
No olvidemos que se trata de valores absolutos. Una correlación lineal de -0,70 también es muy fuerte, pero negativa.
Ahora que hemos comprobado que efectivamente tiene sentido encontrar esa recta (la nube de puntos nos dice que hay correlación, y las matemáticas nos dicen que esa correlación es muy fuerte), podemos ponernos manos a la obra.
Tengamos en cuenta que, tal y como afirman nuestros autores de referencia,
«Aun cuando el coeficiente de correlación lineal mide la fuerza de una relación lineal, no nos dice nada acerca de la relación matemática entre las dos variables» (Johnson & Kuby).
Expresiones algebraicas
Según explica Dolores Lorente en el material del Máster de Big Data & Data Science de la Universidad de Barcelona,
«la relación entre dos variables puede ser
- funcional: cuando existe una función matemática que liga ambas variables (como el radio y el área de un círculo, por ejemplo).
- aleatoria: cuando no existe entre las variables una relación exacta, pero se observa una tendencia en los comportamientos de ambas».
La relación entre las notas y el tiempo de estudio es aleatoria.
Como vimos anteriormente, la relación entre variables no tiene porqué ser lineal:
Cada tipo de relación tiene una expresión algebraica que se ajusta mejor a la nube de puntos. Johnson & Kuby exponen los siguientes ejemplos:
- Relación lineal: $\widehat{y} = b_0 + b_1x$
- Relación cuadrática: $\widehat{y} = a + bx + cx^2$
- Relación exponencial: $\widehat{y} = a(b^x)$
- Relación logarítmica: $\widehat{y} = alog_bx$
Estas expresiones algebraicas «describen la relación matemática entre $x$ e $y$, y reciben el nombre de modelos o ecuaciones de predicción» (Johnson & Kuby).
Como hemos visto, en el caso de las notas y el tiempo de estudio la relación es lineal (para este conjunto de datos simulados), por lo que la expresión algebraica correspondiente es la primera.
Es importante notar que en estas expresiones la variable a predecir se denota por $\widehat{y}$, indicando que se trata de una estimación. Recordemos que la relación es aleatoria y no funcional, por lo que nunca podremos obtener el valor real de $y$. La ecuación de la recta es:
$$ y = ax + b$$
La ecuación de Johnson & Kuby reemplaza $y$ por $\widehat{y}$, $m$ por $b_1$ y $b$ por $b_0$, donde
- $\widehat{y}$ es la estimación de $y$
- $b_0$ es la estimación de $b$ (la ordenada en el origen)
- $b_1$ es la estimación de $a$ (la pendiente de la recta)
En el material del Máster en Big Data & Data Science, Dolores Lorente utiliza una expresión distinta para la relación lineal:
$$ y = \beta_0 + \beta_1x + \varepsilon $$
En esta versión, $y$ representa el valor real de la variable, y $\beta_0$ y $\beta_1$ equivalen a $b$ y $a$, respectivamente, pero en la ecuación se incluye el término epsilon ($\varepsilon$), que representa el error aleatorio de la estimación. En palabras de Lorente:
- «Epsilon ($\varepsilon$) representa la diferencia entre el valor real de $y_{i}$ en una nube de puntos y el valor estimado que proporcionaría la ecuación de la recta.
- $\beta_{0}$: es la ordenada en el origen.
- $\beta_{1}$: es la pendiente (inclinación o tangente) de la recta de regresión. Este coeficiente indica el incremento de unidades de la variable $Y$ que se produce por cada incremento en una unidad de la variable $X$».
James, Witten, Hastie, Tibshirani & Taylor, en su obra An Introduction to Statistical Learning utilizan una expresión general que sirve para cualquier relación (lineal, cuadrática, exponencial, logarítmica, etc):
$$
Y = f(X) + \varepsilon
$$
Aquí, simplemente lo que están diciendo es que los valores de $Y$, están en función de $X$, sin concretar el tipo de función, más un error aleatorio ($\varepsilon $).
Pero $f(X) + \varepsilon$ es una forma de expresar que la función $f$ es una función estimada, y en la misma obra podemos ver:
$$
\widehat{Y} = \widehat{f}(X)
$$
Es decir, los valores estimados de $Y$ dependen de una función estimada de $X$. Como está claro que se trata de valores estimados que provienen de una función estimada, ya no hace falta añadir epsilon ($\varepsilon$). En el caso de la relación lineal, y tomando como base la notación utilizada por Lorente, la expresión sería:
$$
\widehat{y} = \widehat{\beta_0}+ \widehat{\beta_1}x
$$
En esta expresión, que ya se parece más a la de Johnson & Kuby, se enfatiza que la estimación de $y$ ($\widehat{y}$), depende de la estimación de $\beta_0$ y $\beta_1$ ($\widehat{\beta_0}$ y $\widehat{\beta_1}$, respectivamente).
Es importante señalar que $\widehat{\beta_0}$ y $\widehat{\beta_1}$ son estimaciones porque generan la recta de mejor ajuste según los datos que tenemos. En este caso, las notas simuladas de los exámenes de matemáticas y los tiempos de estudio de los alumnos de un instituto concreto, de un año concreto. Aunque hayamos definido ese conjunto de datos como la población, la relación «real» entre las notas y los tiempos de estudio no la conocemos ni la conoceremos nunca. Estamos estimando esa relación, y eso algo aún más evidente cuando se trabaja con muestras, que es lo que suele suceder.
En la blibiografía disponible es frecuente ver $\beta$ en lugar de $\widehat\beta$ cuando se trata de las betas estimadas, para simplificar la notación, pero en puridad $\beta$ sería el parámetro real y no estimado que definiría la relación real entre las variables.
Nota: $X$, $Y$ o $\widehat{Y}$ en mayúsculas representan a todo el conjunto de valores que pueden tomar las variables correspondientes. Las versiones en minúsculas $x_i$ , $y_i$ o $\widehat{y_i}$ represetan a un valor concreto que toman dichas variables. En ocasiones se omite el subíndice $i$ para simplificar la notación.
La recta de regresión o recta de mejor ajuste
Ya sabemos que la expresión algebraica, o el modelo, que mejor casa con la naturaleza de la relación entre notas y tiempo de estudio es la relación lineal:
- $\widehat{y} = b_0 + b_1x$
- $y = \beta_0 + \beta_1x + \varepsilon$
- $\widehat{y} = \widehat{\beta_0}+ \widehat{\beta_1}x$
según la notación que elijamos.
Ahora nuestro trabajo es encontrar la recta que mejor se ajusta a los datos que tenemos y eso se reduce, si elegimos la notación $\widehat{y} = \widehat{\beta_0}+ \widehat{\beta_1}x$, a encontrar las betas adecuadas ($\widehat{\beta_0}$ y $\widehat{\beta_1}$).
El método de mínimos cuadrados
El método de mínimos cuadrados consiste en hallar las constantes $\widehat{\beta_0}$ y $\widehat{\beta_1}$ tales que el sumatorio de las distancias elevadas al cuadrado entre los valores reales y los valores estimados mediante la recta sea la mínima posible. Es decir, se trata de hacer que este sumatorio sea lo más pequeño posible:
$$
\sum (y_i – \widehat{y}_i)^2
$$
El siguiente gráfico permite visualizar dichas distancias, también conocidas como residuos:
Pediente
Para encontrar la pendiente de la recta de mejor ajuste ($\widehat{\beta_1}$ según la notación utilizada por Lorente, o $b_1$ según la elegida por Johnson & Kuby) podemos usar la siguiente fórmula:
$$
\widehat{\beta_1} = \frac{\sum (x_i – \bar{x})(y_i – \bar{y})}{\sum (x_i – \bar{x})^2}
$$
o lo que es lo mismo:
$$ {
\widehat{\beta_1} = \frac{\sigma_{xy}} { \sigma_{x}^2 } }
$$
Ordenada en el origen
Una vez que tenemos la pendiente, $\widehat{\beta_1}$, podemos calcular la ordenada en el origen con la siguiente fórmula:
$$
\widehat{\beta_0} = \frac{\sum y_i – (\widehat{\beta_1}\sum x_i)}{n}
$$
o su versión simplificada:
$$
\widehat{\beta_0} = \bar{y} – \widehat{\beta_1}\bar{x}
$$
El siguiente código muestra como calcular $\widehat{\beta_1}$ con Python paso a paso, sin usar la funciones para la covarianza y la varianza de NumPy.
# Definimos las variables
x = df['tiempo_estudio']
y = df['nota']
N = len(df) # Tamaño de la población (1600)
# 1. Calcular Covarianza Poblacional (sigma_xy)
# Fórmula: Suma de productos de desviaciones / N
numerador = ((x - x.mean()) * (y - y.mean())).sum()
sigma_xy = numerador / N
# 2. Calcular Varianza Poblacional de X (sigma_x^2)
# Fórmula: Suma de distancias al cuadrado / N
denominador = ((x - x.mean())**2).sum()
sigma_x_sq = denominador / N
# 3. Calcular Beta 1
beta_1 = sigma_xy / sigma_x_sq
print(f"Covarianza Poblacional (sigma_xy): {sigma_xy:.4f}")
print(f"Varianza Poblacional de X (sigma_x^2): {sigma_x_sq:.4f}")
print(f"Resultado B1: {beta_1:.5f}")
Covarianza Poblacional (sigma_xy): 43.3403 Varianza Poblacional de X (sigma_x^2): 3696.7309 Resultado B1: 0.01172
$\widehat{\beta_1}$ es 0,01172. Esto significa que, por término medio, cada minuto de estudio hace que la nota aumente 0,01 punto. Parece poco, pero si en lugar de usar minutos pensamos en horas (60 minutos), vemos que cada hora extra de estudio aumenta la nota en unos 0.7 puntos, lo que tiene bastante sentido según los datos con los que estamos trabajando.
Nota importante: en el código precedente hemos dividido por $N$ y no por $N-1$ porque en su momento definimos el conjunto de datos como la «población». En casos reales, en los que normalmente se trabaja con una muestra, debemos dividir por $N-1$.
Ahora es el turno calcular la ordenada en el origen, $\widehat{\beta_0}$:
# Asumiendo que ya tienes B1 calculado del paso anterior
# Si no, B1 = 0.01172
# 1. Calcular las medias
media_x = df['tiempo_estudio'].mean()
media_y = df['nota'].mean()
# 2. Calcular B0
beta_0 = media_y - (beta_1 * media_x)
print(f"Media de Notas (y): {media_y:.4f}")
print(f"Media de Tiempo de Estudio (x): {media_x:.4f}")
print(f"Intercepto (B0): {beta_0:.5f}")
Media de Notas (y): 6.4763 Media de Tiempo de Estudio (x): 270.7856 Intercepto (B0): 3.30164
La ordenada en el origen, o intercepto (donde la recta corta al eje $y$) es 3,30161. Es decir, según nuestro modelo, un alumno que no estudia absolutamente nada para el examen obtendrá, en promedio, un 3,30.
Nuestra ecuación para estimar la nota en función del tiempo de estudio, es la siguiente:
$$
Nota = 3,30 + 0,01 * TiempoEstudio
$$
Explicación
¿Por qué funcionan estas fórmulas? ¿De dónde vienen y cómo podemos estar seguros de que al usarlas estamos encontrando $\widehat{\beta_0}$ y $\widehat{\beta_1}$ que generan la recta de mejor ajuste y minimizan las diferencias al cuadrado entre las notas reales y las estimadas?
Analicemos la expresión que debemos minimizar, $E$, de Error (según la fuente consultada, también puede ser $SSE$: Sum of Squared Errors o, simplemente, $S$):
$$
E = \sum_{i=1}^{n} (y_i – \widehat{y}_i)^2
$$
Al elevar las diferencias al cuadrado evitamos que las diferencias negativas cancelen a las positivas, penalizamos los errores grandes y generamos una función derivable en todos sus puntos. Las dos últimas razones explican por qué no se usa el valor absoluto del error en este caso. Si se usara el valor absoluto, diez errores de 1 unidad los penalizaríamos igual que uno de 10 unidades (por ejemplo) y la función generada tendría forma de V, que no es derivable en el vértice (donde el error es mínimo). Esto último lo entenderemos un poco más adelante.
Hemos visto que:
$$
\widehat{y} = \widehat{\beta_0} + \widehat{\beta_1}x
$$
Por lo tanto:
$$
E = \sum_{i=1}^{n} (y_i – \widehat{y}_i)^2 = \sum_{i=1}^{n} (y_i – (\widehat{\beta_0} + \widehat{\beta_1}x_i))^2 = \sum_{i=1}^{n} (y_i – \widehat{\beta_0}- \widehat{\beta_1}x_i)^2
$$
En matemáticas suele haber más de una forma de obtener los mismos resultados. A partir de $\sum_{i=1}^{n} (y_i – \widehat{\beta_0}- \widehat{\beta_1}x_i)^2$ hay esencialmente dos maneras de llegar a las ecuaciones para obtener $\widehat{\beta_0}$ y $\widehat{\beta_1}$ que minimizan $E$.
El método algebraico
Este método puede verse completamente desarrollado en el paper Simple Linear Regression
Least Squares Estimates of $\beta_0$ and $\beta_1$, publicado en amherst.edu. Éste, a su vez, se basa en el paper de Eric Iksoon titulado A Note On Derivation of the Least Squares Estimator, y publicado por la Universidad de Hawai en 1996.
Se parte de:
$$
E = \sum_{i=1}^{n} (y_i – \widehat{\beta_0}- \widehat{\beta_1}x_i)^2 = \sum_{i=1}^{n}[(y_i + \bar{y} – \bar{y})-\widehat{\beta_0}-\widehat{\beta_1}(x_i+\bar{x}-\bar{x})]^2
$$
y se desarrolla algebraicamente la expresión hasta llegar a:
$$
E = n(\bar{y} – \widehat{\beta_0} – \widehat{\beta_1}\bar{x})^2 + (\widehat{\beta_1} -\frac{\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^{n} (x_i – \bar{x})^2})^2 + \sum_{i=1}^{n}(y_i – \bar{y})^2(1-[\frac{\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^{n} (x_i – \bar{x})^2 \sum_{i=1}^{n}(y_i – \bar{y})^2}]^2)
$$
Esto reduce $E$ a la suma de tres términos. El primero incluye $\widehat{\beta_0}$ y $\widehat{\beta_1}$, el segundo incluye $\widehat{\beta_1}$, y el tercero depende sólo de los datos, y no incluye los parámetros buscados.
Tanto el primer como el segundo término están elevados al cuadrado, por lo que no pueden ser menores que cero, y toda la expresión anterior solo puede ser mayor o igual que el tercer término, que es el mínimo valor posible de $E$:
$$
\sum_{i=1}^{n}(y_i – \bar{y})^2(1-[\frac{\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^{n} (x_i – \bar{x})^2 \sum_{i=1}^{n}(y_i – \bar{y})^2}]^2)
$$
Para que $E$ sea igual a la expresión anterior, los primeros dos términos deben ser iguales a cero.
$$
0 = n(\bar{y} – \widehat{\beta_0} – \widehat{\beta_1}\bar{x})^2
$$
$$
0 = (\widehat{\beta_1} -\frac{\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^{n} (x_i – \bar{x})^2})^2
$$
La primera ecuación nos da:
$$
0 = n(\bar{y} – \widehat{\beta_0} – \widehat{\beta_1}\bar{x})^2
$$
$$
⇒ 0 = \bar{y} – \widehat{\beta_0} – \widehat{\beta_1}\bar{x}
$$
$$
⇒ \widehat{\beta_0} = \bar{y} – \widehat{\beta_1}\bar{x}
$$
De la segunda ecuación obtenemos:
$$
0 = (\widehat{\beta_1} -\frac{\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^{n} (x_i – \bar{x})^2})^2
$$
$$
⇒ 0 = \widehat{\beta_1} -\frac{\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^{n} (x_i – \bar{x})^2}
$$
$$
⇒ \widehat{\beta_1} = \frac{\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^{n} (x_i – \bar{x})^2}
$$
Como puede comprobarse, las ecuaciones finales son las mismas que mostramos antes.
Deducción mediante derivadas parciales
El método anterior es muy claro y tiene la ventaja de que no obliga a tener conocimientos de cálculo para resolver el problema. Como desventaja, a parte de lo engorroso que es, podemos decir que dificulta la «visualización» de lo que estamos haciendo.
Con éste método, el punto de partida es exactamente el mismo que antes:
$$
E = \sum_{i=1}^{n} (y_i – \widehat{\beta_0}- \widehat{\beta_1}x_i)^2
$$
Para visualizar el concepto en dos dimensiones, vamos a simplicar el problema, siguiendo el ejemplo de Dolores Lorente. Supongamos que tenemos una nube de puntos cuya recta de mejor ajuste pasa por el origen. En ese caso, $\widehat{\beta_0}=0$, y
$$
E = \sum_{i=1}^{n} (y_i – \widehat{\beta_1}x_i)^2
$$
Si reordenamos y desarrollamos la expresión, tenemos:
$$
E = \sum_{i=1}^{n} (\widehat{\beta_1}^2x_i^2-2\widehat{\beta_1}x_iy_i+y_i^2) = (\sum_{i=1}^{n}x_i^2)\widehat{\beta_1}^2 – (2\sum_{i=1}^{n}x_iy_i)\widehat{\beta_1} +(\sum_{i=1}^{n}y_i^2)
$$
Si nos fijamos bien, y como dice Lorente, la expresión de $E$ como función de $\widehat{\beta_1}$ es una función del tipo
$$
f(x) = Ax^2 + Bx + C
$$
donde
$$
A = \sum_{i=1}^{n}x_i^2, B = 2\sum_{i=1}^{n}x_iy_i, C = \sum_{i=1}^{n}y_i^2
$$
Este tipo de funciones generan una parábola, y si el coeficiente $A$ es positivo, la parábola tendrá concavidad positiva (forma de U). Una función con concavidad positiva también se denomina función convexa:
Sabemos que $E$ es una función convexa porque el coeficiente A, que multiplica $\widehat{\beta_1}$, es
$$
\sum_{i=1}^{n}x_i^2 > 0
$$
Por lo tanto, en este caso simplificado con $\widehat{\beta_0} = 0$, el problema se reduce a encontrar el punto en el que la suma de los errores al cuadrado es la mínima posible. Dicho punto se halla en el valor de $\widehat{\beta_1}$ donde la derivada es $0$:
Ahora que lo hemos «visto», es más fácil entender lo que sigue.
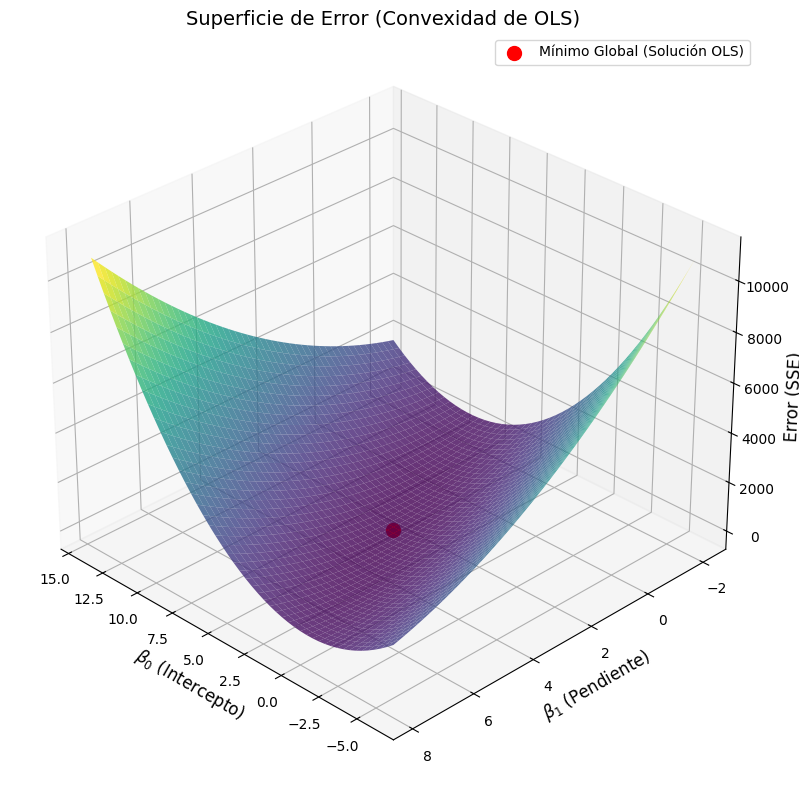
Normalmente, la recta que mejor se ajusta a una nube de puntos no pasa por el origen, por lo que $\widehat{\beta_0}$ no es $0$, y $E$ no es una parábola, si no una superficie convexa generada por $\widehat{\beta_0}$ y $\widehat{\beta_1}$:
En este caso, debemos hallar las derivadas parciales con respecto a $\widehat{\beta_0}$ y $\widehat{\beta_1}$, de $E$.
Recordemos que:
$$
E = \sum_{i=1}^{n} (y_i – \widehat{\beta_0} – \widehat{\beta_1}x_i)^2
$$
Para minimizar $E$, primero igualamos a cero la derivada parcial con respecto a $\widehat{\beta_0}$.
$$
\frac{\partial E}{\partial \widehat{\beta}_0} = \sum_{i=1}^{n} 2(y_i – \widehat{\beta}_0 – \widehat{\beta}_1 x_i)(-1) = 0
$$
Simplificando (dividiendo entre $-2$):
$$
\sum_{i=1}^{n} (y_i – \widehat{\beta}_0 – \widehat{\beta}_1 x_i) = 0$$$$\sum y_i – n\widehat{\beta}_0 – \widehat{\beta}_1 \sum x_i = 0
$$
Dividimos por $n$ y despejamos $\widehat{\beta}_0$, y obtenemos la primera ecuación:
$$
\widehat{\beta}_0 = \bar{y} – \widehat{\beta}_1 \bar{x}
$$
Luego repetimos el proceso para la pendiente $\widehat{\beta}_1$:
$$
\frac{\partial E}{\partial \widehat{\beta}_1} = \sum_{i=1}^{n} 2(y_i – \widehat{\beta}_0 – \widehat{\beta}_1 x_i)(-x_i) = 0$$
Simplificando:
$$
\sum_{i=1}^{n} (x_i y_i – \widehat{\beta}_0 x_i – \widehat{\beta}_1 x_i^2) = 0
$$
Dividimos por $n$, sustituimos $\widehat{\beta}_0$ y resolvemos para $\widehat{\beta}_1$, y llegamos a la segunda ecuación:
$$
\widehat{\beta}_1 = \frac{\sum (x_i – \bar{x})(y_i – \bar{y})}{\sum (x_i – \bar{x})^2}
$$
Soluciones de segundo orden
Aunque parece que todo a terminado aquí, porque hemos llegado a las mismas ecuaciones de dos formas distintas, y con el método algebraico ya había quedado claro que estábamos minimizando $E$, cuando usamos el método de derivadas parciales nos queda algo por hacer.
Las derivadas de primer orden son cero en los puntos mínimos, pero también en los puntos máximos y los puntos de silla. Por lo tanto, debemos asegurarnos de que la solución que hemos encontrado (donde las derivadas son cero) es realmente un mímino.
En el caso de una una sola variable, basta con comprobar que la segunda derivada es positiva (la función es una parábola convexa, con forma de U).
Que la segunda derivada sea positiva, significa la tasa de cambio de las pendientes es positiva. Si camino por la U desde la derecha primero voy bajando, hasta llegar al mínimo, donde es cero, para luego empezar a subir. La pendiente al principio del camino es, $-5$, luego $-1$, luego $0$, luego $+1$, luego $+5$… Los números están creciendo: la pendiente está aumentando. Su tasa de cambio es positiva.
Si trabajamos con más variables, como $\widehat\beta_0$ y $\widehat\beta_1$, se usa una matriz de segundas derivadas denominada Matriz Hessiana.
La Hessiana, en este caso, es una matriz cuadrada $2 \times 2$ que contiene todas las segundas derivadas parciales posibles de la función de error $E$.
$$ H = \begin{bmatrix}
\frac{\partial^2 E}{\partial \beta_0^2} & \frac{\partial^2 E}{\partial \beta_0 \partial \beta_1} \\
\frac{\partial^2 E}{\partial \beta_1 \partial \beta_0} & \frac{\partial^2 E}{\partial \beta_1^2}
\end{bmatrix} $$
Si desarrollamos esta matriz, obtenemos:
$$H = \begin{bmatrix}
2n & 2\sum x_i \\
2\sum x_i & 2\sum x_i^2
\end{bmatrix}$$
Para verificar que los parámetros hallados realmente nos dan el punto mínimo de la función, debemos asegurarnos de que la matriz es Definida Positiva, lo que se cumple si:
- El primer elemento diagonal es positivo.
- El determinante de la matriz es positivo.
La condición $2n > 0$ es siempre cierta, puesto que el tamaño de la muestra siempre es positivo.
Por su parte, el determinante de esta matriz es:
$$|H| = 4n \sum (x_i – \bar{x})^2$$
La suma de cuadrados es siempre positiva (salvo que los valores de $x$ sean todos idénticos), por lo que el determinante es positivo.
Esto confirma que los valores $\widehat\beta_0$ y $\widehat\beta_1$ que hemos encontrado corresponden a un mínimo global de error.
La importancia de la visualización de los datos
Cuando nos enfrentemos a un caso similar al descrito, y queramos estimar el valor de una variable a partir de otra, siempre debemos empezar por visualizar la nube de puntos.
El famoso «cuarteto de Anscombe» demuestra que conjuntos de datos con prácticamente las mismas propiedades (media aritmética, varianza de los valores de $x$ e $y$, correlación, coeficiente de correlación y recta de regresión lineal), pueden ser completamente distintos. Los datos de ejemplo, publicados por Anscombe en 1973 son los siguientes:
| I | II | III | IV | |||||
|---|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | x | y | |
| 0 | 10.00 | 8.04 | 10.00 | 9.14 | 10.00 | 7.46 | 8.00 | 6.58 |
| 1 | 8.00 | 6.95 | 8.00 | 8.14 | 8.00 | 6.77 | 8.00 | 5.76 |
| 2 | 13.00 | 7.58 | 13.00 | 8.74 | 13.00 | 12.74 | 8.00 | 7.71 |
| 3 | 9.00 | 8.81 | 9.00 | 8.77 | 9.00 | 7.11 | 8.00 | 8.84 |
| 4 | 11.00 | 8.33 | 11.00 | 9.26 | 11.00 | 7.81 | 8.00 | 8.47 |
| 5 | 14.00 | 9.96 | 14.00 | 8.10 | 14.00 | 8.84 | 8.00 | 7.04 |
| 6 | 6.00 | 7.24 | 6.00 | 6.13 | 6.00 | 6.08 | 8.00 | 5.25 |
| 7 | 4.00 | 4.26 | 4.00 | 3.10 | 4.00 | 5.39 | 19.00 | 12.50 |
| 8 | 12.00 | 10.84 | 12.00 | 9.13 | 12.00 | 8.15 | 8.00 | 5.56 |
| 9 | 7.00 | 4.82 | 7.00 | 7.26 | 7.00 | 6.42 | 8.00 | 7.91 |
| 10 | 5.00 | 5.68 | 5.00 | 4.74 | 5.00 | 5.73 | 8.00 | 6.89 |
Cada uno de estos grupos presentan las siguientes propiedades:
| Propiedad | Valor |
|---|---|
| Media de cada una de las variables x | 9.0 |
| Varianza de cada una de las variables x | 11.0 |
| Media de cada una de las variables y | 7.5 |
| Varianza de cada una de las variables y | 4.12 |
| Correlación entre cada una de las variables x e y | 0.816 |
| Recta de regresión | y = 3 + 0.5x |
A pesar de estas similitudes, al graficar los datos vemos que hay grandes diferencias entre los grupos:
import matplotlib.pyplot as plt
import numpy as np
# Datos oficiales del Cuarteto de Anscombe
# Los valores X son iguales para los primeros 3 datasets
x = np.array([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5])
# Dataset 1: Relación lineal simple
y1 = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68])
# Dataset 2: Relación no lineal (curva)
y2 = np.array([9.14, 8.14, 8.74, 8.77, 9.26, 8.10, 6.13, 3.10, 9.13, 7.26, 4.74])
# Dataset 3: Relación lineal con un outlier (punto atípico)
y3 = np.array([7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73])
# Dataset 4: Relación vertical con un outlier extremo
# Este dataset tiene sus propios valores de X
x4 = np.array([8, 8, 8, 8, 8, 8, 8, 19, 8, 8, 8])
y4 = np.array([6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.50, 5.56, 7.91, 6.89])
# Preparamos la estructura para iterar
datasets = [
(x, y1, "I: Linealidad Limpia"),
(x, y2, "II: Falta de Linealidad (Curva)"),
(x, y3, "III: Impacto de un Outlier"),
(x4, y4, "IV: Falsa Correlación por Outlier")
]
# Configuración del gráfico (2 filas, 2 columnas)
fig, axes = plt.subplots(2, 2, figsize=(12, 10), sharex=True, sharey=True)
axes = axes.flatten() # Aplanamos para iterar fácilmente
for i, (data_x, data_y, titulo) in enumerate(datasets):
ax = axes[i]
# 1. Graficar los puntos
ax.scatter(data_x, data_y, color='teal', s=80, alpha=0.7, edgecolors='k')
# 2. Calcular y dibujar la línea de regresión
# Ajuste polinómico de grado 1 (línea recta: y = mx + b)
m, b = np.polyfit(data_x, data_y, 1)
# Generamos puntos para dibujar la línea roja
x_line = np.linspace(2, 20, 100)
y_line = m * x_line + b
ax.plot(x_line, y_line, color='red', linestyle='--', linewidth=2, label=f'Regresión (igual en todos)')
# 3. Estética
ax.set_title(titulo, fontsize=14, fontweight='bold')
ax.grid(True, linestyle=':', alpha=0.6)
# Para el Dataset IV, ampliamos un poco el eje X para ver bien el punto lejano
if i == 3:
ax.set_xlim(2, 20)
# Etiquetas generales
fig.text(0.5, 0.02, 'Variable X', ha='center', fontsize=12)
fig.text(0.02, 0.5, 'Variable Y', va='center', rotation='vertical', fontsize=12)
plt.tight_layout(rect=[0.03, 0.03, 1, 1]) # Ajuste para dejar espacio a las etiquetas generales
plt.show()
Una última reflexión
Para llegar hasta aquí hemos tenido que escribir previamente nueve artículos, algunos de ellos de una extensión considerable. Empezamos a escalar desde la base, definiendo variables y repasando conceptos estadísticos de sobra conocidos, como la media, la moda y la desviación típica. Revisamos distintas opciones para graficar los datos, definimos formalmente la curva normal y nos adentramos en el análisis bivariado, donde estudiamos la covarianza y la correlación lineal.
En este artículo ha aparecido por primera vez la palabra «modelo«, para referirse a lo que Johnson & Kuby denominan también «ecuaciones de predicción». Este no es el final del camino, evidentente. Todavía queda mucha montaña por encima de nuestras cabezas. Podríamos decir que estamos en el campo base.
Aunque hasta ahora la filosofía ha sido ir ascendiendo paso a paso, sin mencionar nada que no se hubiese explicado antes, aquí hemos dado un salto introduciendo algo de álgebra y cálculo diferencial. El propósito de esta serie de artículos no es enseñar cálculo (ni álgebra), si no ciencia de datos. Pero la ciencia de datos se apoya en otras disciplinas y a veces es necesario, para poder seguir avanzando, dar ciertas cosas por sabidas.
En algún punto del camino haremos una pausa para añadir anexos que traten estos temas, enfocándolos en su aplicación directa a la ciencia de datos. Ahí repasaremos algunas nociones de álgrebra y cálculo, empezando por la operativa básica, continuando con la definción del concepto de función y terminando derivación e integración.
Tarde o tempranos tendremos que repasar, también, la operativa matricial. Pero no nos adelantemos; ya cruzaremos ese puente.
Bibliografía y referencias
- Johnson, R. & Kuby, P. Estadística elemental: lo esencial (10a ed.). Cengage Learning Editores S.A. (2008).
- James G, Witten D, Hastie T, Tibshirani R, Taylor J. An introduction to statistical learning: With applications in python. 2023.a ed. Cham, Suiza: Springer International Publishing; 2024.
- Simple Linear Regression Least Squares Estimates of β0 and β1 [citado 5 de febrero de 2026]. Disponible en: https://www.amherst.edu/system/files/media/1287/SLR_Leastsquares.pdf
- Iksoon, E. A Note On Derivation of the Least Squares Estimator [citado 5 de febrero de 2026]. Disponible en: https://www.economics.hawaii.edu/research/workingpapers/88-98/WP_96-11.pdf
- Lorente, D. Demostracion_Minimos_Cuadrados [citado 5 de febrero de 2026]. Diponible en https://github.com/md-lorente/documentation/blob/master/Demostracion_Minimos_Cuadrados.pdf
- Ruiz, C. Análisis matemático básico. Convexidad y concavidad [citado 12 de febrero de 2026]. Departamento de Analisis Matemático, Facultad de Matemáticas, Universidad Complutense de Madrid. Disponible en: https://blogs.mat.ucm.es/cruizb/wp-content/uploads/sites/48/2023/02/M-Derivadas-6-B.pdf
- Wikipedia contributors. Cuarteto de Anscombe [Internet]. Wikipedia, The Free Encyclopedia. Disponible en: https://es.wikipedia.org/w/index.php?title=Cuarteto_de_Anscombe&oldid=147794477
Para el desarrollo del método por derivadas parciales (planteamiento y desarrollo de fórmulas), hemos hecho uso de Gemini Pro 3.0 que, a su vez, se basa en varias fuentes:
- Wooldridge, J. M. (2015). Introductory Econometrics: A Modern Approach. Cengage Learning. (Capítulo 2: El modelo de regresión lineal simple).
- Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012). Introduction to Linear Regression Analysis. Wiley.
- Gujarati, D. N., & Porter, D. C. (2011). Econometría. McGraw-Hill.
Para la explicación de las derivadas de segundo orden y la matriz Hessiana, las fuentes principales de Gemini han sido la siguientes:
- Chiang, A. C., & Wainwright, K. (2006). Fundamental Methods of Mathematical Economics (4th Edition). McGraw-Hill.
- Simon, C. P., & Blume, L. (1994). Mathematics for Economists. W. W. Norton & Company.
- Greene, W. H. (2018). Econometric Analysis (8th Edition). Pearson.
La explicación sencilla sobre las derivadas de segundo orden y porqué permiten saber si estamos ante mínimos o máximos también ha sido planteada por Gemini Pro 3.0 (ya estaba cansado, y no se me ocurría una forma más intuitiva de explicarlo). Para esto, Gemini ha usado las siguientes fuentes:
- Stewart, J. (2015). Cálculo: Trascendentes tempranas. Sección: Calculus I – The Shape of a Graph, Part II (Concavity). Cengage Learning.
- Calculus I – the shape of a graph, part II [Internet]. Lamar.edu. [citado 13 de febrero de 2026]. Disponible en: https://tutorial.math.lamar.edu/classes/calci/shapeofgraphptii.aspx
Artículo anterior: <— Dos variables cuantitativas. Correlación lineal