Felipe Maggi
Lenguaje de programación: Python
- Data Science I: Población, muestra, experimentos y tipos de variables.
- Data Science II-A: Estadística descriptiva unidimensional. Tablas de frecuencia y gráficos de distribución.
- Data Science II-B: Estadística descriptiva unidimensional. Medidas de tendencia central.
- Data Science II-C: Estadística descriptiva unidimensional. Medidas de dispersión.
- Data Science II-D: Estadística descriptiva unidimensional. Medidas de posición.
- Data Science II-E: Estadística descriptiva unidimensional. La curva nornal
Para cada uno de estos temas hay mucha bibliografía disponible, y nos hemos guiado, en parte, por lo expuesto en el material del Máster de Big Data & Data Science de la Universidad de Barcelona, por Dolores Lorente.
Los conceptos estadísticos son de dominio general, pero cuando tengamos que recurrir a una forma concreta de plantear las cosas, haremos uso, mayoritariamente, de las definiciones expuestas en el libro Estadística general: lo esencial, de Johnson & Kuby.
Conjunto de datos
Antes de continuar, vamos a recuperar el conjunto de datos simulados con los que hemos estado trabajando en toda esta serie de artículos.
import pandas as pd
import numpy as np
import random
import string
# Establecer semillas para la reproducibilidad
np.random.seed(42)
random.seed(42)
# Función para generar id_estudiante alfanuméricos aleatorios
def generar_id_estudiante(n):
ids = []
for _ in range(n):
id_estudiante = ''.join(random.choices(string.ascii_uppercase +
string.digits, k=8))
ids.append(id_estudiante)
return ids
# Generar datos
num_estudiantes_por_grupo = 40
total_estudiantes = num_estudiantes_por_grupo * 4
num_notas = 10
ids = generar_id_estudiante(total_estudiantes)
asignatura = 'Matemáticas'
temas = [f'Tema {i+1}' for i in range(num_notas)]
fecha_inicio = pd.Timestamp('2024-09-01')
# Función para generar tiempo de estudio con correlación positiva con notas
def generar_tiempo_estudio(notas, media=270, sd=60, correlacion=0.75):
ruido = np.random.normal(0, sd, len(notas))
tiempo_estudio = media + correlacion * (notas - np.mean(notas)) + ruido
return tiempo_estudio.clip(60, 480).astype(int)
# Generar las notas, fechas y otras columnas
data = {
'id_estudiante': [],
'asignatura': [],
'tema': [],
'fecha': [],
'nota': [],
'calificacion': [],
'estatura': [],
'sexo': [],
'tiempo_estudio': [],
'grupo': []
}
# Grupos disponibles
grupos = ['A', 'B', 'C', 'D']
num_grupos = len(grupos)
# Asignar aleatoriamente los estudiantes a los grupos
grupo_asignado = np.repeat(grupos, num_estudiantes_por_grupo)
random.shuffle(grupo_asignado)
for idx, id_estudiante in enumerate(ids):
fechas = [fecha_inicio + pd.DateOffset(weeks=i*4) for i in range(num_notas)]
notas = np.random.normal(6.5, 1, num_notas).clip(0, 10)
estatura = np.random.uniform(150, 190, num_notas)
sexo = random.choice(['H', 'M'])
tiempo_estudio = generar_tiempo_estudio(notas)
for i in range(num_notas):
data['id_estudiante'].append(id_estudiante)
data['asignatura'].append(asignatura)
data['tema'].append(temas[i])
data['fecha'].append(fechas[i])
data['nota'].append(round(notas[i], 2))
# Asignar calificación basada en la nota
if 9 <= notas[i] <= 10:
calificacion = 'sobresaliente'
elif 7 <= notas[i] < 9:
calificacion = 'notable'
elif 5 <= notas[i] < 7:
calificacion = 'aprobado'
else:
calificacion = 'suspenso'
data['calificacion'].append(calificacion)
data['estatura'].append(estatura[i])
data['sexo'].append(sexo)
data['tiempo_estudio'].append(tiempo_estudio[i])
data['grupo'].append(grupo_asignado[idx])
# Crear el DataFrame
df = pd.DataFrame(data)
# Añadir la columna "aprobado"
df['aprobado'] = df['calificacion'].apply(lambda x: 0 if x == 'suspenso' else 1)
# Mostrar el DataFrame
print(df)
id_estudiante asignatura tema fecha nota calificacion \
0 XAJI0Y6D Matemáticas Tema 1 2024-09-01 7.00 aprobado
1 XAJI0Y6D Matemáticas Tema 2 2024-09-29 6.36 aprobado
2 XAJI0Y6D Matemáticas Tema 3 2024-10-27 7.15 notable
3 XAJI0Y6D Matemáticas Tema 4 2024-11-24 8.02 notable
4 XAJI0Y6D Matemáticas Tema 5 2024-12-22 6.27 aprobado
... ... ... ... ... ... ...
1595 FNKOMV2X Matemáticas Tema 6 2025-01-19 4.28 suspenso
1596 FNKOMV2X Matemáticas Tema 7 2025-02-16 7.87 notable
1597 FNKOMV2X Matemáticas Tema 8 2025-03-16 5.41 aprobado
1598 FNKOMV2X Matemáticas Tema 9 2025-04-13 7.76 notable
1599 FNKOMV2X Matemáticas Tema 10 2025-05-11 7.45 notable
estatura sexo tiempo_estudio grupo aprobado
0 157.272999 H 357 C 1
1 157.336180 H 256 C 1
2 162.169690 H 274 C 1
3 170.990257 H 185 C 1
4 167.277801 H 236 C 1
... ... ... ... ... ...
1595 173.907293 M 252 A 0
1596 184.787835 M 250 A 1
1597 185.633286 M 299 A 1
1598 167.961510 M 189 A 1
1599 168.372148 M 284 A 1
[1600 rows x 11 columns]
Datos bivariados
Nuestros autores de referencia definen los datos bivariados como
«los valores de dos variables diferentes, que se obtienen del mismo elemento poblacional» (Johnson & Kuby).
Los mismos autores explican que «cada una de las dos variables puede ser cualitativa o cuantitativa. En consecuencia, tres combinaciones de tipos de variables pueden formar datos bivariados:
- Ambas variables son cualitativas.
- Una variable es cualitativa y la otra es cuantitativa.
- Ambas variables son cuantitativas».
Variables cualitativas
Si tomamos como ejemplo nuestro conjunto datos, podemos observar que tenemos ocho variables cualitativas (de atributo o categóricas):
- ID de estudiante
- Asignatura
- Tema
- Fecha*
- Calificación
- Sexo
- Grupo
- Aprobado**
*En este contexto, la fecha puede considerarse como una variable cualitativa ordinal. Sin embargo, y dependiendo del uso, también se puede tratar como una variable cuantitativa continua.
**Aprobado es una variable engañosa, porque toma los valores 0 y 1, que son numéricos, y uno podría creer que se trata de una variable cuantitativa. Sin embargo, debemos pensar que los ceros son «no», y los unos son «sí». Si hacemos eso, es fácil ver que se trata de una variable nominal dicotómica.
Para más detalles con respecto a los tipos de variables, recomendamos repasar el primer artículo de esta serie.
Variables cuantitativas
En cuanto a las variables cuantitativas, en nuestro conjunto de datos encontramos:
- Nota
- Estatura
- Tiempo de estudio
Las tres son variables continuas, aunque se presenten como discretas (las notas, por ejemplo, están redondeadas a 2 decimales y el tiempo de estudio se presenta en minutos, como números enteros). Que se presenten discretizadas, no quiere decir que la variable sea discreta.
Tabulación cruzada, tabla de contingencia o tabla de doble entrada
Cuando se trata de «dos variables cualitativas (de atributo o categóricas), es frecuente que los datos se ordenen en una tabulación cruzada o tabla de contingencia» (Johnson & Kuby).
Por ejemplo, podríamos cruzar el tema (tema 1, tema 2, tema 3…) con la calificación (aprobado, notable, suspenso, sobresaliente), y analizar de esta forma si existe alguna relación entre la calificación y los temas (quizá hay temas más fáciles que otros, que tienen una proporción mayor de aprobados, notables y sobresalientes).
También podríamos analizar conjuntamente grupo y aprobado, para ver si hay diferencias entre aprobados y suspensos según el grupo.
Hay otras combinaciones posibles como sexo y grupo, incluso tema y grupo (aunque esta última no aportaría información relevante).
A continuación, vamos crear una tabla de contingencia para tema y calificación:
# --- Creación de la Tabla de Contingencia ---
# Para ordenar los temas correctamente, convertimos la columna a tipo categórico ordenado
df['tema'] = pd.Categorical(df['tema'], categories=[f'Tema {i+1}' for i in range(num_notas)], ordered=True)
# X (índice) será el 'tema', Y (columnas) será la 'calificacion'
# Añadimos margins=True para incluir los totales y margins_name para nombrar la fila/columna de totales
tabla_contingencia = pd.crosstab(index=df['tema'], columns=df['calificacion'], margins=True, margins_name="Total")
# Mostrar la tabla de contingencia con totales
print("--- Tabla de Contingencia (Tema vs. Calificación) con Totales ---")
print(tabla_contingencia)
calificacion aprobado notable sobresaliente suspenso Total tema Tema 1 91 54 2 13 160 Tema 2 99 47 1 13 160 Tema 3 115 32 0 13 160 Tema 4 104 43 1 12 160 Tema 5 102 46 0 12 160 Tema 6 93 54 3 10 160 Tema 7 94 51 1 14 160 Tema 8 101 45 0 14 160 Tema 9 95 55 0 10 160 Tema 10 103 44 1 12 160 Total 997 471 9 123 1600
Repasemos qué contiene nuestro conjunto de datos, antes de analizar esta tabla y ponerle nombres a las cosas: tal como se explica en el primer artículo de la serie, tenemos en nuestras manos las notas de matemáticas de 160 estudiantes (40 estudiantes por grupo, y 4 grupos) de segundo de bachillerato de un instituto concreto, obtenidas en los exámenes de cada uno de los temas (10 temas). En total, 1600 notas:
$$40*4*10=1600$$
Aunque lo que vamos a ver a continuación se aplica a este ejemplo, basado en dos variables cualitativas, también sirve para el caso de una variable cualitativa y otra cuantitativa. Veremos los detalles en el artículo correspondiente.
Distribución conjunta
Basándonos en lo que explica Dolores Lorente en el material del Máster en Big Data & Data Science de la Universidad de Barcelona, estamos tratando
«con una población de $n$ individuos ($N$, si trabajamos con la población), para los que estamos estudiando dos características simultáneamente ($X$ e $Y$), cada una con modalidades $x_{1},x_{2}, x_{3}, \ldots x_{k}$ e $y_{1},y_{2}, y_{3}, \ldots y_{p}$ respectivamente. Entonces, las observaciones correspondientes a cada individuo son el par $(x_{i}, y_{j}) \quad con \quad i = 1,2,3 \ldots k, \quad j = 1,2,3 \ldots p \quad siendo \quad k,p \in \Bbb N $«
Pero cuidado, es fácil confundirse, y pensar que los individuos son los estudiantes. Pero hay 160 estudiantes, y tenemos 1600 datos. Lo que estamos estudiando son los resultados de cada examen (que son los $n$ individuos), distribuidos por tema ($X$), y calificación ($Y$).
En las filas tenemos los temas ($X$) y en las columnas, las calificaciones ($Y$). Los números ($n_{ij}$) representan la cantidad de veces que se observa un par ($x_i$, $y_j$). Así, por ejemplo:
$n_{6,3} = 3$, porque el par ($x_6$, $y_3$), que es el par (tema 6, sobresaliente), aparece tres veces en el conjunto de datos. En la siguiente tabla incluimos las etiquetas $x_i$ e $y_i$ correspondientes, y destacamos el par ($x_6$, $y_3$):
# --- Creación de la Tabla de Contingencia ---
# Para ordenar los temas correctamente, convertimos la columna a tipo categórico ordenado
df['tema'] = pd.Categorical(df['tema'], categories=[f'Tema {i+1}' for i in range(num_notas)], ordered=True)
# Ordenar las calificaciones para asegurar que 'sobresaliente' sea y_3
# crosstab respeta el orden de las categorías
categorias_calificacion = ['aprobado', 'notable', 'sobresaliente', 'suspenso']
df['calificacion'] = pd.Categorical(df['calificacion'], categories=categorias_calificacion, ordered=True)
# X (índice) será el 'tema', Y (columnas) será la 'calificacion'
# Añadimos margins=True para incluir los totales
tabla_contingencia_tema_calif = pd.crosstab(index=df['tema'], columns=df['calificacion'], margins=True, margins_name='Total')
# --- Formatear celdas con etiquetas n_ij en LaTeX ---
# Crear una copia para formatear con strings sin modificar la original numérica
tabla_formateada = tabla_contingencia_tema_calif.copy().astype(object)
# Iterar sobre las celdas de datos (excluyendo la fila y columna de Total)
for i in range(tabla_formateada.shape[0] - 1):
for j in range(tabla_formateada.shape[1] - 1):
valor_celda = tabla_contingencia_tema_calif.iloc[i, j]
# Crear la etiqueta n_ij en formato LaTeX (sin paréntesis explícitos)
tabla_formateada.iloc[i, j] = f'{valor_celda} $n_{{{i+1},{j+1}}}$'
# --- Añadir etiquetas a los totales marginales ---
# Totales marginales de filas (última columna)
for i in range(tabla_formateada.shape[0] - 1):
valor_celda = tabla_contingencia_tema_calif.iloc[i, -1]
tabla_formateada.iloc[i, -1] = f'{valor_celda} $n_{{{i+1}.}}$'
# Totales marginales de columnas (última fila)
for j in range(tabla_formateada.shape[1] - 1):
valor_celda = tabla_contingencia_tema_calif.iloc[-1, j]
tabla_formateada.iloc[-1, j] = f'{valor_celda} $n_{{.{j+1}}}$'
# Total general (esquina inferior derecha)
valor_celda = tabla_contingencia_tema_calif.iloc[-1, -1]
# Se usa n.. como notación estándar para el total general (suma sobre i y j)
tabla_formateada.iloc[-1, -1] = f'{valor_celda} $N_{{..}}$'
# --- Añadir etiquetas LaTeX y Resaltar la celda específica (x_6, y_3) ---
# Separar los nombres de los datos de los totales para etiquetar correctamente
nombres_filas_datos = tabla_contingencia_tema_calif.index[:-1]
nombres_columnas_datos = tabla_contingencia_tema_calif.columns[:-1]
# Crear las nuevas etiquetas combinando el nombre original y la etiqueta LaTeX (sin paréntesis explícitos)
nuevas_etiquetas_filas = [f'{nombre} $x_{{{i+1}}}$' for i, nombre in enumerate(nombres_filas_datos)] + ['Total']
nuevas_etiquetas_columnas = [f'{nombre} $y_{{{j+1}}}$' for j, nombre in enumerate(nombres_columnas_datos)] + ['Total']
# Asignar las nuevas etiquetas al DataFrame formateado
tabla_formateada.index = nuevas_etiquetas_filas
tabla_formateada.columns = nuevas_etiquetas_columnas
tabla_formateada.index.name = 'Tema'
tabla_formateada.columns.name = 'Calificación'
# Función para resaltar la celda usando las nuevas etiquetas LaTeX
def resaltar_celda(data):
# Crear un DataFrame del mismo tamaño para los estilos
df_estilo = pd.DataFrame('', index=data.index, columns=data.columns)
# Definir las etiquetas a buscar de forma programática y segura
# Las llaves dobles {{}} son necesarias para crear llaves literales {} dentro de un f-string
# y asegurar que la cadena coincida exactamente con la etiqueta generada.
fila_a_resaltar = f'Tema 6 $x_{{6}}$'
columna_a_resaltar = f'sobresaliente $y_{{3}}$'
# Comprobar si las etiquetas existen antes de aplicar el estilo para mayor seguridad
if fila_a_resaltar in df_estilo.index and columna_a_resaltar in df_estilo.columns:
df_estilo.loc[fila_a_resaltar, columna_a_resaltar] = 'background-color: yellow; color: black'
return df_estilo
# Aplicar el estilo a la tabla de contingencia formateada
tabla_resaltada = tabla_formateada.style.apply(resaltar_celda, axis=None)
# Mostrar la tabla de contingencia con la celda resaltada y nuevas etiquetas
print("--- Tabla de Contingencia (Tema vs. Calificación) con totales, etiquetas y celda resaltada ---")
display(tabla_resaltada)
--- Tabla de Contingencia (Tema vs. Calificación) con totales, etiquetas y celda resaltada ---
| Calificación | aprobado $y_{1}$ | notable $y_{2}$ | sobresaliente $y_{3}$ | suspenso $y_{4}$ | Total |
|---|---|---|---|---|---|
| Tema | |||||
| Tema 1 $x_{1}$ | 91 $n_{1,1}$ | 54 $n_{1,2}$ | 2 $n_{1,3}$ | 13 $n_{1,4}$ | 160 $n_{1.}$ |
| Tema 2 $x_{2}$ | 99 $n_{2,1}$ | 47 $n_{2,2}$ | 1 $n_{2,3}$ | 13 $n_{2,4}$ | 160 $n_{2.}$ |
| Tema 3 $x_{3}$ | 115 $n_{3,1}$ | 32 $n_{3,2}$ | 0 $n_{3,3}$ | 13 $n_{3,4}$ | 160 $n_{3.}$ |
| Tema 4 $x_{4}$ | 104 $n_{4,1}$ | 43 $n_{4,2}$ | 1 $n_{4,3}$ | 12 $n_{4,4}$ | 160 $n_{4.}$ |
| Tema 5 $x_{5}$ | 102 $n_{5,1}$ | 46 $n_{5,2}$ | 0 $n_{5,3}$ | 12 $n_{5,4}$ | 160 $n_{5.}$ |
| Tema 6 $x_{6}$ | 93 $n_{6,1}$ | 54 $n_{6,2}$ | 3 $n_{6,3}$ | 10 $n_{6,4}$ | 160 $n_{6.}$ |
| Tema 7 $x_{7}$ | 94 $n_{7,1}$ | 51 $n_{7,2}$ | 1 $n_{7,3}$ | 14 $n_{7,4}$ | 160 $n_{7.}$ |
| Tema 8 $x_{8}$ | 101 $n_{8,1}$ | 45 $n_{8,2}$ | 0 $n_{8,3}$ | 14 $n_{8,4}$ | 160 $n_{8.}$ |
| Tema 9 $x_{9}$ | 95 $n_{9,1}$ | 55 $n_{9,2}$ | 0 $n_{9,3}$ | 10 $n_{9,4}$ | 160 $n_{9.}$ |
| Tema 10 $x_{10}$ | 103 $n_{10,1}$ | 44 $n_{10,2}$ | 1 $n_{10,3}$ | 12 $n_{10,4}$ | 160 $n_{10.}$ |
| Total | 997 $n_{.1}$ | 471 $n_{.2}$ | 9 $n_{.3}$ | 123 $n_{.4}$ | 1600 $N_{..}$ |
En resumen, $n_{ij}$ representa la frecuencia absoluta del par ($x_i$, $y_j$). Esto significa que sólo hubo 3 sobresalientes entre todas las calificaciones del tema 6.
Las columnas de totales (conocidas como totales marginales o, simplemente, marginales) representan los totales de cada fila ($n_{i.}$) y los totales de cada columna ($n_{.j}$). Su nombre deriva del hecho de que se encuentran en los márgenes de la tabla.
En este caso concreto, los totales de filas son todos iguales (160), puesto que, de cada tema, se calificaron 160 exámenes (4 grupos, de 40 alumnos cada grupo).
Los totales de las columnas varían, y representan el total de aprobados, notables, sobresalientes y suspensos.
La suma de los valores de los totales marginales de las filas es 1600, y la suma de los valores de los totales marginales de las columnas también es 1600. En otras palabras, el total de totales, o gran total ($N_{..}$ en la tabla), es igual tamaño poblacional. Si estuviésemos tratando con una muestra, hablaríamos de tamaño muestral, y de $n$ en lugar de $N$:
$$
\sum_{i=1}^{k}\sum_{j=1}^{p} n_{ij} = N
$$
Tabla de frecuencias relativas
Porcentajes basados en el gran total
Si en la tabla anterior dividimos todos los valores por el gran total, obtenemos las frecuencias relativas de cada uno de ellos.
«Se llama frecuencia relativa del par $ (x_{i}, y_{j})$ a la proporción de individuos en la población que presentan, simultáneamente, la modalidad $x_{i}$ y la modalidad $y_{j}$. Se representa matemáticamente como $f_{ij}$» (Lorente).
La fórmula de la frecuencia relativa es:
$$
f_{ij}= \frac{n_{ij}}{N}
$$
De nuevo, es importante recalcar que dividimos por $N$ y no por $n$, porque estamos trabajando con la población, en este caso.
# --- Creación de la Tabla de Contingencia ---
# Para ordenar los temas correctamente, convertimos la columna a tipo categórico ordenado
df['tema'] = pd.Categorical(df['tema'], categories=[f'Tema {i+1}' for i in range(num_notas)], ordered=True)
# Ordenar las calificaciones para asegurar que 'sobresaliente' sea y_3
# crosstab respeta el orden de las categorías
categorias_calificacion = ['aprobado', 'notable', 'sobresaliente', 'suspenso']
df['calificacion'] = pd.Categorical(df['calificacion'], categories=categorias_calificacion, ordered=True)
# X (índice) será el 'tema', Y (columnas) será la 'calificacion'
# Se calcula la tabla de frecuencias relativas con normalize='all'
tabla_relativa = pd.crosstab(index=df['tema'], columns=df['calificacion'], margins=True, margins_name='Total', normalize='all')
# --- Formatear celdas con etiquetas f_ij en LaTeX ---
# Crear una copia para formatear con strings sin modificar la original numérica
tabla_formateada = tabla_relativa.copy().astype(object)
# Iterar sobre las celdas de datos (excluyendo la fila y columna de Total)
for i in range(tabla_formateada.shape[0] - 1):
for j in range(tabla_formateada.shape[1] - 1):
valor_celda = tabla_relativa.iloc[i, j]
# Formatear la frecuencia relativa como porcentaje y añadir la etiqueta f_ij
tabla_formateada.iloc[i, j] = f'{valor_celda:.2%} $f_{{{i+1},{j+1}}}$'
# --- Añadir etiquetas a los totales marginales ---
# Totales marginales de filas (última columna)
for i in range(tabla_formateada.shape[0] - 1):
valor_celda = tabla_relativa.iloc[i, -1]
tabla_formateada.iloc[i, -1] = f'{valor_celda:.2%} $f_{{{i+1}.}}$'
# Totales marginales de columnas (última fila)
for j in range(tabla_formateada.shape[1] - 1):
valor_celda = tabla_relativa.iloc[-1, j]
tabla_formateada.iloc[-1, j] = f'{valor_celda:.2%} $f_{{.{j+1}}}$'
# Total general (esquina inferior derecha)
valor_celda = tabla_relativa.iloc[-1, -1]
# Se usa f.. como notación estándar para el total general (suma sobre i y j)
tabla_formateada.iloc[-1, -1] = f'{valor_celda:.2%} $f_{{..}}$'
# --- Añadir etiquetas LaTeX y Resaltar la celda específica (x_6, y_3) ---
# Separar los nombres de los datos de los totales para etiquetar correctamente
nombres_filas_datos = tabla_relativa.index[:-1]
nombres_columnas_datos = tabla_relativa.columns[:-1]
# Crear las nuevas etiquetas combinando el nombre original y la etiqueta LaTeX (sin paréntesis explícitos)
nuevas_etiquetas_filas = [f'{nombre} $x_{{{i+1}}}$' for i, nombre in enumerate(nombres_filas_datos)] + ['Total']
nuevas_etiquetas_columnas = [f'{nombre} $y_{{{j+1}}}$' for j, nombre in enumerate(nombres_columnas_datos)] + ['Total']
# Asignar las nuevas etiquetas al DataFrame formateado
tabla_formateada.index = nuevas_etiquetas_filas
tabla_formateada.columns = nuevas_etiquetas_columnas
tabla_formateada.index.name = 'Tema'
tabla_formateada.columns.name = 'Calificación'
# Función para resaltar la celda usando las nuevas etiquetas LaTeX
def resaltar_celda(data):
# Crear un DataFrame del mismo tamaño para los estilos
df_estilo = pd.DataFrame('', index=data.index, columns=data.columns)
# Definir las etiquetas a buscar de forma programática y segura
# Las llaves dobles {{}} son necesarias para crear llaves literales {} dentro de un f-string
# y asegurar que la cadena coincida exactamente con la etiqueta generada.
fila_a_resaltar = f'Tema 6 $x_{{6}}$'
columna_a_resaltar = f'sobresaliente $y_{{3}}$'
# Comprobar si las etiquetas existen antes de aplicar el estilo para mayor seguridad
if fila_a_resaltar in df_estilo.index and columna_a_resaltar in df_estilo.columns:
df_estilo.loc[fila_a_resaltar, columna_a_resaltar] = 'background-color: yellow; color: black'
return df_estilo
# Aplicar el estilo a la tabla de contingencia formateada
tabla_resaltada = tabla_formateada.style.apply(resaltar_celda, axis=None)
# Mostrar la tabla de contingencia con la celda resaltada y nuevas etiquetas
print("--- Tabla de Contingencia (Tema vs. Calificación) con Frecuencias Relativas ---")
display(tabla_resaltada)
--- Tabla de Contingencia (Tema vs. Calificación) con Frecuencias Relativas ---
| Calificación | aprobado $y_{1}$ | notable $y_{2}$ | sobresaliente $y_{3}$ | suspenso $y_{4}$ | Total |
|---|---|---|---|---|---|
| Tema | |||||
| Tema 1 $x_{1}$ | 5.69% $f_{1,1}$ | 3.38% $f_{1,2}$ | 0.12% $f_{1,3}$ | 0.81% $f_{1,4}$ | 10.00% $f_{1.}$ |
| Tema 2 $x_{2}$ | 6.19% $f_{2,1}$ | 2.94% $f_{2,2}$ | 0.06% $f_{2,3}$ | 0.81% $f_{2,4}$ | 10.00% $f_{2.}$ |
| Tema 3 $x_{3}$ | 7.19% $f_{3,1}$ | 2.00% $f_{3,2}$ | 0.00% $f_{3,3}$ | 0.81% $f_{3,4}$ | 10.00% $f_{3.}$ |
| Tema 4 $x_{4}$ | 6.50% $f_{4,1}$ | 2.69% $f_{4,2}$ | 0.06% $f_{4,3}$ | 0.75% $f_{4,4}$ | 10.00% $f_{4.}$ |
| Tema 5 $x_{5}$ | 6.38% $f_{5,1}$ | 2.88% $f_{5,2}$ | 0.00% $f_{5,3}$ | 0.75% $f_{5,4}$ | 10.00% $f_{5.}$ |
| Tema 6 $x_{6}$ | 5.81% $f_{6,1}$ | 3.38% $f_{6,2}$ | 0.19% $f_{6,3}$ | 0.62% $f_{6,4}$ | 10.00% $f_{6.}$ |
| Tema 7 $x_{7}$ | 5.88% $f_{7,1}$ | 3.19% $f_{7,2}$ | 0.06% $f_{7,3}$ | 0.88% $f_{7,4}$ | 10.00% $f_{7.}$ |
| Tema 8 $x_{8}$ | 6.31% $f_{8,1}$ | 2.81% $f_{8,2}$ | 0.00% $f_{8,3}$ | 0.88% $f_{8,4}$ | 10.00% $f_{8.}$ |
| Tema 9 $x_{9}$ | 5.94% $f_{9,1}$ | 3.44% $f_{9,2}$ | 0.00% $f_{9,3}$ | 0.62% $f_{9,4}$ | 10.00% $f_{9.}$ |
| Tema 10 $x_{10}$ | 6.44% $f_{10,1}$ | 2.75% $f_{10,2}$ | 0.06% $f_{10,3}$ | 0.75% $f_{10,4}$ | 10.00% $f_{10.}$ |
| Total | 62.31% $f_{.1}$ | 29.44% $f_{.2}$ | 0.56% $f_{.3}$ | 7.69% $f_{.4}$ | 100.00% $f_{..}$ |
Como puede comprobarse, la frecuencia relativa de $(x_6, y_3$) es del 0.19%. Es decir, la combinación «tema 6 y sobresaliente» representa menos de un 0.2% del conjunto total de datos.
Por otro lado, es fácil ver que la suma de las frecuencias relativas marginales es igual a 1 (100%), si estamos trabajando en porcentajes:
$$ \sum_{i=1}^{k}\sum_{j=1}^{p} f_{ij} = \frac{1}{n}\sum_{i=1}^{k}\sum_{j=1}^{p} n_{ij} = 1
$$
Distribuciones marginales
Los porcentajes totales en los márgenes de la tabla se conocen como distribuciones marginales, y se corresponden con los porcentajes de cada una de las variables, independientemente de la otra.
En palabras de Lorente, las distribuciones marginales son «distribuciones unidimensionales extraídas de datos bidimensionales«.
Ya hemos visto las frecuencias absolutas marginales son $n_{i.}$ en el caso de las filas, y $n_{.j}$ para el caso de las columnas. Por lo tanto, las frecuencias relativas marginales son:
- $ f_{i.} = \frac{n_{i.}}{N}$ en el caso de las filas.
- $ f_{.j} = \frac{n_{.j}}{N}$ en el caso de las columnas.
Su utilidad radica en que nos permiten ver los datos correspondientes a cada variable, independientemente de la otra, lo que viene a ser equivalente a analizar la variable por sí sola. Por tanto, es aplicable todo lo visto anteriormente con respecto al análisis univariable.
Frecuencias relativas condicionadas
Porcentajes basados en el total de filas
Supongamos que, en lugar de querer saber qué porcentaje sobre el total de los datos representa la combinación «tema 6 y sobresaliente» $(x_6, y_3$), queremos saber el porcentaje de sobresalientes en los exámenes del tema 6.
Es decir, queremos saber cómo se distribuyen las calificaciones, dado un tema en concreto. Esto se conoce como distribución condicionada.
Parafraseando a Lorente, «aunque se pueden obtener las frecuencias absolutas condicionadas, es mucho más útil calcular las frecuencias relativas condicionadas. Lo que queremos obtener es la frecuencia relativa de $Y$ (las calificaciones), dado que $X$ (los temas) tienen un valor determinado ($x_i$)«. En notación matemática, según se expone en el Material del Máster en Big Data & Data Science de la Universidad de Barcelona, las frecuencias relativas de $Y|X = x_i$ son:
$ \quad \quad \quad f_{j|i} = \frac{n_{ij}}{n_{i.}}
\quad \text{donde} \quad
0 \leq f_{j|i} \leq 1 \quad y \quad \sum_{i=1}^{k}f_{j|i}=1
$
Esto se lee así: la frecuencia de $j$ (que representa la calificaciones) dado $i$ (que representa a los temas), es igual a la frecuencia absoluta de $(x_i, y_j)$, dividida por la frecuencia absoluta marginal de $i$. Dicha frecuencia está entre $0$ y $1$, y la suma de todas ellas es igual a $1$.
En la práctica, y aplicando los expuesto por Johnson & Kuby, simplemente se trata de dividir los valores por el total de las filas, en lugar de hacerlo por el gran total. El resultado es una tabla como la que sigue:
# --- Creación de la Tabla de Contingencia ---
# Para ordenar los temas correctamente, convertimos la columna a tipo categórico ordenado
df['tema'] = pd.Categorical(df['tema'], categories=[f'Tema {i+1}' for i in range(num_notas)], ordered=True)
# Ordenar las calificaciones para asegurar que 'sobresaliente' sea y_3
# crosstab respeta el orden de las categorías
categorias_calificacion = ['aprobado', 'notable', 'sobresaliente', 'suspenso']
df['calificacion'] = pd.Categorical(df['calificacion'], categories=categorias_calificacion, ordered=True)
# X (índice) será el 'tema', Y (columnas) será la 'calificacion'
# --- CORRECCIÓN: Se calculan las frecuencias relativas por fila manualmente para asegurar que los totales sean 100% ---
# 1. Calcular tabla de frecuencias absolutas con totales
tabla_absoluta = pd.crosstab(index=df['tema'], columns=df['calificacion'], margins=True, margins_name='Total')
# 2. Crear una tabla de frecuencias relativas dividiendo cada celda por el total de su fila
# .div() con axis=0 divide cada valor de la fila por el valor correspondiente en la Serie (el total de la fila)
tabla_relativa = tabla_absoluta.div(tabla_absoluta["Total"], axis=0)
# --- Formatear celdas con etiquetas f_ij en LaTeX ---
# Crear una copia para formatear con strings sin modificar la original numérica
tabla_formateada = tabla_relativa.copy().astype(object)
# Iterar sobre las celdas de datos (excluyendo la fila y columna de Total)
for i in range(tabla_formateada.shape[0] - 1):
for j in range(tabla_formateada.shape[1] - 1):
valor_celda = tabla_relativa.iloc[i, j]
# Usar la notación de frecuencia condicional f(y_j | x_i)
tabla_formateada.iloc[i, j] = f'{valor_celda:.2%} $f_{{{j+1}|{i+1}}}$'
# --- Añadir etiquetas a los totales marginales ---
# Totales marginales de filas (última columna)
for i in range(tabla_formateada.shape[0] - 1):
valor_celda = tabla_relativa.iloc[i, -1] # Este valor ahora es 1.0
tabla_formateada.iloc[i, -1] = f'{valor_celda:.2%} $f_{{{i+1}.}}$'
# Totales marginales de columnas (última fila)
for j in range(tabla_formateada.shape[1] - 1):
valor_celda = tabla_relativa.iloc[-1, j] # Estos son los f_.j
tabla_formateada.iloc[-1, j] = f'{valor_celda:.2%} $f_{{.{j+1}}}$'
# Total general (esquina inferior derecha)
valor_celda = tabla_relativa.iloc[-1, -1] # Este valor ahora es 1.0
tabla_formateada.iloc[-1, -1] = f'{valor_celda:.2%} $f_{{..}}$'
# --- Añadir etiquetas LaTeX y Resaltar la celda específica (x_6, y_3) ---
# Separar los nombres de los datos de los totales para etiquetar correctamente
nombres_filas_datos = tabla_relativa.index[:-1]
nombres_columnas_datos = tabla_relativa.columns[:-1]
# Crear las nuevas etiquetas combinando el nombre original y la etiqueta LaTeX (sin paréntesis explícitos)
nuevas_etiquetas_filas = [f'{nombre} $x_{{{i+1}}}$' for i, nombre in enumerate(nombres_filas_datos)] + ['Total']
nuevas_etiquetas_columnas = [f'{nombre} $y_{{{j+1}}}$' for j, nombre in enumerate(nombres_columnas_datos)] + ['Total']
# Asignar las nuevas etiquetas al DataFrame formateado
tabla_formateada.index = nuevas_etiquetas_filas
tabla_formateada.columns = nuevas_etiquetas_columnas
tabla_formateada.index.name = 'Tema'
tabla_formateada.columns.name = 'Calificación'
# Función para resaltar la celda usando las nuevas etiquetas LaTeX
def resaltar_celda(data):
# Crear un DataFrame del mismo tamaño para los estilos
df_estilo = pd.DataFrame('', index=data.index, columns=data.columns)
# Definir las etiquetas a buscar de forma programática y segura
# Las llaves dobles {{}} son necesarias para crear llaves literales {} dentro de un f-string
# y asegurar que la cadena coincida exactamente con la etiqueta generada.
fila_a_resaltar = f'Tema 6 $x_{{6}}$'
columna_a_resaltar = f'sobresaliente $y_{{3}}$'
# Comprobar si las etiquetas existen antes de aplicar el estilo para mayor seguridad
if fila_a_resaltar in df_estilo.index and columna_a_resaltar in df_estilo.columns:
df_estilo.loc[fila_a_resaltar, columna_a_resaltar] = 'background-color: yellow; color: black'
return df_estilo
# Aplicar el estilo a la tabla de contingencia formateada
tabla_resaltada = tabla_formateada.style.apply(resaltar_celda, axis=None)
# Mostrar la tabla de contingencia con la celda resaltada y nuevas etiquetas
print("--- Tabla de Contingencia (Tema vs. Calificación) con Frecuencias Relativas por Fila ---")
display(tabla_resaltada)
--- Tabla de Contingencia (Tema vs. Calificación) con Frecuencias Relativas por Fila ---
| Calificación | aprobado $y_{1}$ | notable $y_{2}$ | sobresaliente $y_{3}$ | suspenso $y_{4}$ | Total |
|---|---|---|---|---|---|
| Tema | |||||
| Tema 1 $x_{1}$ | 56.88% $f_{1|1}$ | 33.75% $f_{2|1}$ | 1.25% $f_{3|1}$ | 8.12% $f_{4|1}$ | 100.00% $f_{1.}$ |
| Tema 2 $x_{2}$ | 61.88% $f_{1|2}$ | 29.38% $f_{2|2}$ | 0.62% $f_{3|2}$ | 8.12% $f_{4|2}$ | 100.00% $f_{2.}$ |
| Tema 3 $x_{3}$ | 71.88% $f_{1|3}$ | 20.00% $f_{2|3}$ | 0.00% $f_{3|3}$ | 8.12% $f_{4|3}$ | 100.00% $f_{3.}$ |
| Tema 4 $x_{4}$ | 65.00% $f_{1|4}$ | 26.88% $f_{2|4}$ | 0.62% $f_{3|4}$ | 7.50% $f_{4|4}$ | 100.00% $f_{4.}$ |
| Tema 5 $x_{5}$ | 63.75% $f_{1|5}$ | 28.75% $f_{2|5}$ | 0.00% $f_{3|5}$ | 7.50% $f_{4|5}$ | 100.00% $f_{5.}$ |
| Tema 6 $x_{6}$ | 58.13% $f_{1|6}$ | 33.75% $f_{2|6}$ | 1.88% $f_{3|6}$ | 6.25% $f_{4|6}$ | 100.00% $f_{6.}$ |
| Tema 7 $x_{7}$ | 58.75% $f_{1|7}$ | 31.87% $f_{2|7}$ | 0.62% $f_{3|7}$ | 8.75% $f_{4|7}$ | 100.00% $f_{7.}$ |
| Tema 8 $x_{8}$ | 63.12% $f_{1|8}$ | 28.12% $f_{2|8}$ | 0.00% $f_{3|8}$ | 8.75% $f_{4|8}$ | 100.00% $f_{8.}$ |
| Tema 9 $x_{9}$ | 59.38% $f_{1|9}$ | 34.38% $f_{2|9}$ | 0.00% $f_{3|9}$ | 6.25% $f_{4|9}$ | 100.00% $f_{9.}$ |
| Tema 10 $x_{10}$ | 64.38% $f_{1|10}$ | 27.50% $f_{2|10}$ | 0.62% $f_{3|10}$ | 7.50% $f_{4|10}$ | 100.00% $f_{10.}$ |
| Total | 62.31% $f_{.1}$ | 29.44% $f_{.2}$ | 0.56% $f_{.3}$ | 7.69% $f_{.4}$ | 100.00% $f_{..}$ |
Como podemos observar, el porcentaje de sobresalientes en los exámenes del tema 6, es del 1.88%. La etiqueta junto al valor correspondiente ($f_{3|6}$) se lee así: 1.88% es la frecuencia relativa de sobresalientes ($y=3$), dado que el tema es el 6 ($x=6$)
Nótese que en esta tabla la suma de los totales de las columnas es 100%, y cada uno de los valores representa el porcentaje de cada una de las calificaciones. Por ejemplo, el 29.44% de los exámenes se calificó con un notable. Estos porcentajes marginales son los mismos que los de la tabla obtenida al calcular las frecuencias relativas en función del gran total. No pasa lo mismo con los totales de las filas, que ya no tiene sentido sumar.
Porcentajes basados en el total de columnas
Supongamos ahora que lo que queremos saber, dada una calificación $Y$, los porcentajes de cada tema ($X$). Esto responde a la pregunta, por ejemplo, ¿en qué tema se ha registrado el mayor porcentaje de sobresalientes? Aquí, lo que nos interesa saber es cómo se distribuyen los temas entre las calificaciones.
Si volvemos a la notación matemática (recurriendo otra vez al material del Máster), tenemos que las frecuencias relativas de $X|Y = y_j$ son:
$ \quad \quad \quad f_{i|j} = \frac{n_{ij}}{n_{.j}}
\quad \text{donde} \quad
0 \leq f_{i|j} \leq 1 \quad y \quad \sum_{j=1}^{p}f_{i|j}=1
$
De nuevo, y en la práctica, el ejercicio es mucho más simple: debemos dividir las frecuencias absolutas de la tabla original por el total de las columnas, en lugar de hacerlo por el gran total.
# --- Creación de la Tabla de Contingencia ---
# Para ordenar los temas correctamente, convertimos la columna a tipo categórico ordenado
df['tema'] = pd.Categorical(df['tema'], categories=[f'Tema {i+1}' for i in range(num_notas)], ordered=True)
# Ordenar las calificaciones para asegurar que 'sobresaliente' sea y_3
# crosstab respeta el orden de las categorías
categorias_calificacion = ['aprobado', 'notable', 'sobresaliente', 'suspenso']
df['calificacion'] = pd.Categorical(df['calificacion'], categories=categorias_calificacion, ordered=True)
# X (índice) será el 'tema', Y (columnas) será la 'calificacion'
# --- CORRECCIÓN: Se calculan las frecuencias relativas por columna manualmente para asegurar que los totales sean 100% ---
# 1. Calcular tabla de frecuencias absolutas con totales
tabla_absoluta = pd.crosstab(index=df['tema'], columns=df['calificacion'], margins=True, margins_name='Total')
# 2. Crear una tabla de frecuencias relativas dividiendo cada celda por el total de su columna
# .div() con axis=1 divide cada valor de la columna por el valor correspondiente en la Serie (el total de la columna)
tabla_relativa = tabla_absoluta.div(tabla_absoluta.loc['Total'], axis=1)
# --- Formatear celdas con etiquetas f_ij en LaTeX ---
# Crear una copia para formatear con strings sin modificar la original numérica
tabla_formateada = tabla_relativa.copy().astype(object)
# Iterar sobre las celdas de datos (excluyendo la fila y columna de Total)
for i in range(tabla_formateada.shape[0] - 1):
for j in range(tabla_formateada.shape[1] - 1):
valor_celda = tabla_relativa.iloc[i, j]
# Usar la notación de frecuencia condicional f(x_i | y_j)
tabla_formateada.iloc[i, j] = f'{valor_celda:.2%} $f_{{{i+1}|{j+1}}}$'
# --- Añadir etiquetas a los totales marginales ---
# Totales marginales de filas (última columna)
# Estos valores ahora son la frecuencia marginal de la fila f_i.
for i in range(tabla_formateada.shape[0] - 1):
valor_celda = tabla_absoluta.iloc[i, -1] / tabla_absoluta.iloc[-1, -1]
tabla_formateada.iloc[i, -1] = f'{valor_celda:.2%} $f_{{{i+1}.}}$'
# Totales marginales de columnas (última fila)
for j in range(tabla_formateada.shape[1] - 1):
valor_celda = tabla_relativa.iloc[-1, j] # Este valor ahora es 1.0
# La suma de cada distribución condicional es 100%
tabla_formateada.iloc[-1, j] = f'{valor_celda:.2%}'
# Total general (esquina inferior derecha)
tabla_formateada.iloc[-1, -1] = f'{tabla_relativa.iloc[-1, -1]:.2%} $f_{{..}}$'
# --- Añadir etiquetas LaTeX y Resaltar la celda específica (x_6, y_3) ---
# Separar los nombres de los datos de los totales para etiquetar correctamente
nombres_filas_datos = tabla_relativa.index[:-1]
nombres_columnas_datos = tabla_relativa.columns[:-1]
# Crear las nuevas etiquetas combinando el nombre original y la etiqueta LaTeX (sin paréntesis explícitos)
nuevas_etiquetas_filas = [f'{nombre} $x_{{{i+1}}}$' for i, nombre in enumerate(nombres_filas_datos)] + ['Total']
nuevas_etiquetas_columnas = [f'{nombre} $y_{{{j+1}}}$' for j, nombre in enumerate(nombres_columnas_datos)] + ['Total']
# Asignar las nuevas etiquetas al DataFrame formateado
tabla_formateada.index = nuevas_etiquetas_filas
tabla_formateada.columns = nuevas_etiquetas_columnas
tabla_formateada.index.name = 'Tema'
tabla_formateada.columns.name = 'Calificación'
# Función para resaltar la celda usando las nuevas etiquetas LaTeX
def resaltar_celda(data):
# Crear un DataFrame del mismo tamaño para los estilos
df_estilo = pd.DataFrame('', index=data.index, columns=data.columns)
# Definir las etiquetas a buscar de forma programática y segura
# Las llaves dobles {{}} son necesarias para crear llaves literales {} dentro de un f-string
# y asegurar que la cadena coincida exactamente con la etiqueta generada.
fila_a_resaltar = f'Tema 6 $x_{{6}}$'
columna_a_resaltar = f'sobresaliente $y_{{3}}$'
# Comprobar si las etiquetas existen antes de aplicar el estilo para mayor seguridad
if fila_a_resaltar in df_estilo.index and columna_a_resaltar in df_estilo.columns:
df_estilo.loc[fila_a_resaltar, columna_a_resaltar] = 'background-color: yellow; color: black'
return df_estilo
# Aplicar el estilo a la tabla de contingencia formateada
tabla_resaltada = tabla_formateada.style.apply(resaltar_celda, axis=None)
# Mostrar la tabla de contingencia con la celda resaltada y nuevas etiquetas
print("--- Tabla de Contingencia (Tema vs. Calificación) con Frecuencias Relativas por Columna ---")
display(tabla_resaltada)
| Calificación | aprobado $y_{1}$ | notable $y_{2}$ | sobresaliente $y_{3}$ | suspenso $y_{4}$ | Total |
|---|---|---|---|---|---|
| Tema | |||||
| Tema 1 $x_{1}$ | 9.13% $f_{1|1}$ | 11.46% $f_{1|2}$ | 22.22% $f_{1|3}$ | 10.57% $f_{1|4}$ | 10.00% $f_{1.}$ |
| Tema 2 $x_{2}$ | 9.93% $f_{2|1}$ | 9.98% $f_{2|2}$ | 11.11% $f_{2|3}$ | 10.57% $f_{2|4}$ | 10.00% $f_{2.}$ |
| Tema 3 $x_{3}$ | 11.53% $f_{3|1}$ | 6.79% $f_{3|2}$ | 0.00% $f_{3|3}$ | 10.57% $f_{3|4}$ | 10.00% $f_{3.}$ |
| Tema 4 $x_{4}$ | 10.43% $f_{4|1}$ | 9.13% $f_{4|2}$ | 11.11% $f_{4|3}$ | 9.76% $f_{4|4}$ | 10.00% $f_{4.}$ |
| Tema 5 $x_{5}$ | 10.23% $f_{5|1}$ | 9.77% $f_{5|2}$ | 0.00% $f_{5|3}$ | 9.76% $f_{5|4}$ | 10.00% $f_{5.}$ |
| Tema 6 $x_{6}$ | 9.33% $f_{6|1}$ | 11.46% $f_{6|2}$ | 33.33% $f_{6|3}$ | 8.13% $f_{6|4}$ | 10.00% $f_{6.}$ |
| Tema 7 $x_{7}$ | 9.43% $f_{7|1}$ | 10.83% $f_{7|2}$ | 11.11% $f_{7|3}$ | 11.38% $f_{7|4}$ | 10.00% $f_{7.}$ |
| Tema 8 $x_{8}$ | 10.13% $f_{8|1}$ | 9.55% $f_{8|2}$ | 0.00% $f_{8|3}$ | 11.38% $f_{8|4}$ | 10.00% $f_{8.}$ |
| Tema 9 $x_{9}$ | 9.53% $f_{9|1}$ | 11.68% $f_{9|2}$ | 0.00% $f_{9|3}$ | 8.13% $f_{9|4}$ | 10.00% $f_{9.}$ |
| Tema 10 $x_{10}$ | 10.33% $f_{10|1}$ | 9.34% $f_{10|2}$ | 11.11% $f_{10|3}$ | 9.76% $f_{10|4}$ | 10.00% $f_{10.}$ |
| Total | 100.00% | 100.00% | 100.00% | 100.00% | 100.00% $f_{..}$ |
Esta tabla nos dice, por ejemplo, que de todos los sobresalientes, el 33.33% se obtuvieron en los exámenes del tema 6. De forma análoga al caso anterior, la etiqueta junto al valor se lee así: 33.33 % es la frecuencia relativa del tema 6 ($x=6$), dado que la calificación es sobresaliente ($y=3$).
Ahora, la suma de las frecuencias marginales de las filas es 100%, pero ya no tiene sentido sumar los totales marginales de las columnas.
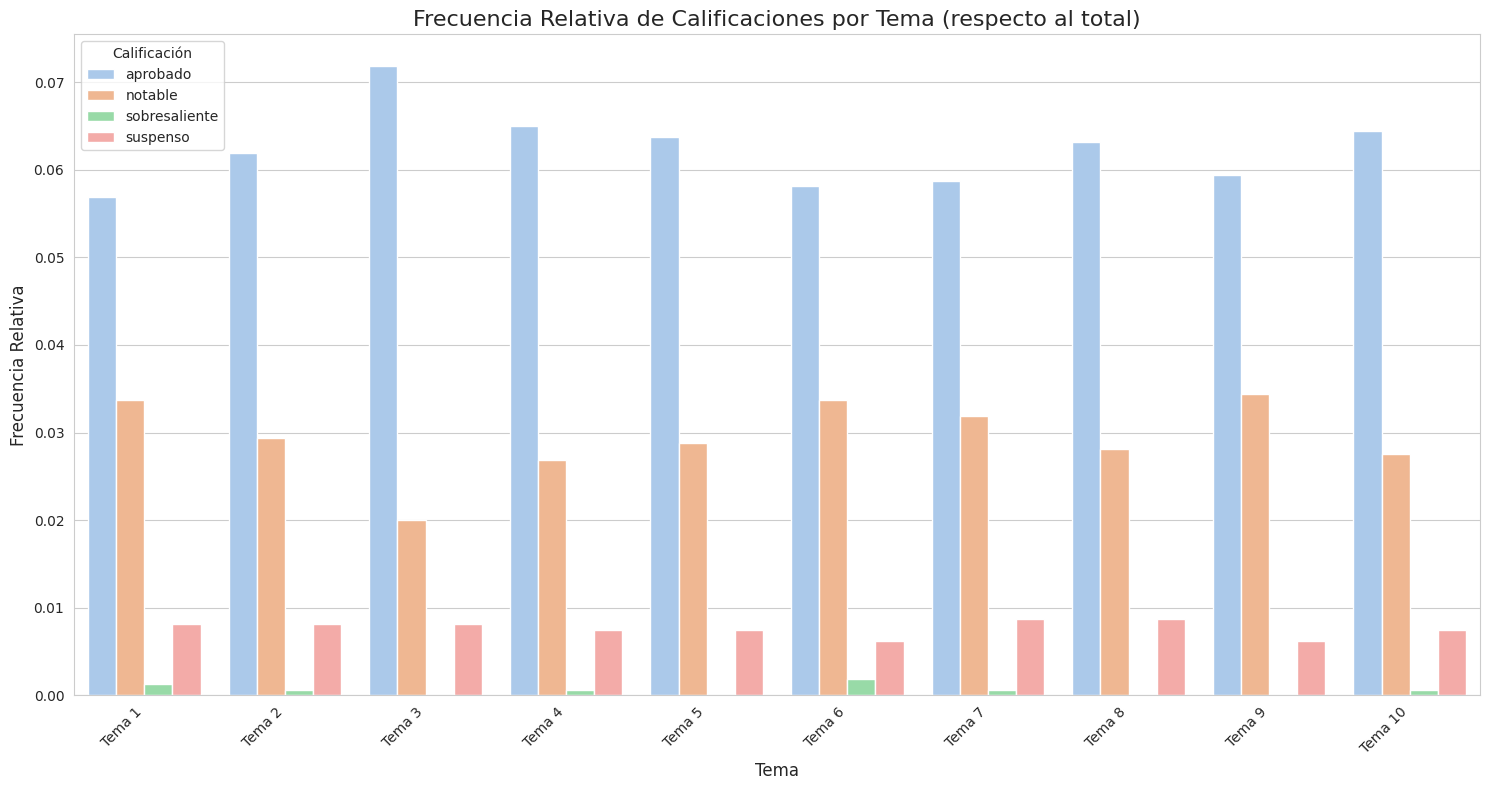
Representación gráfica
Cuando se trata de dos variables cualitativas, como es el caso, la representación visual más adecuada son los gráficos de barras.
El siguiente gráfico muestra las frecuencias basadas en el gran total de aprobados, notables, sobresalientes y suspensos por tema.
Importante: al mostrar los datos según su porcentaje respecto al gran total, no se trata de frecuencias condicionadas. Dejamos como ejercicio graficar las frecuencias relativas condicionadas por tema y calificación.
import matplotlib.pyplot as plt
import seaborn as sns
# --- Creación del Gráfico de Barras ---
# 1. Calcular la tabla de contingencia con frecuencias relativas al total
tabla_relativa_total = pd.crosstab(
index=df['tema'],
columns=df['calificacion'],
normalize='all' # Frecuencias relativas al gran total
)
# 2. Reorganizar los datos para que sean compatibles con seaborn
# Usamos stack() para convertir las columnas en una nueva columna de índice,
# y luego reset_index() para convertir los índices en columnas.
datos_grafico = tabla_relativa_total.stack().reset_index(name='frecuencia_relativa')
# 3. Crear el gráfico
plt.figure(figsize=(15, 8)) # Ajustar el tamaño para mejor legibilidad
sns.set_style("whitegrid") # Añadir un estilo al gráfico
barplot = sns.barplot(
data=datos_grafico,
x='tema',
y='frecuencia_relativa',
hue='calificacion',
palette='pastel' # Usar una paleta de colores agradable
)
# 4. Añadir títulos y etiquetas
plt.title('Frecuencia Relativa de Calificaciones por Tema (respecto al total)', fontsize=16)
plt.xlabel('Tema', fontsize=12)
plt.ylabel('Frecuencia Relativa', fontsize=12)
plt.xticks(rotation=45, ha='right') # Rotar las etiquetas del eje x para que no se solapen
plt.legend(title='Calificación')
plt.tight_layout() # Ajustar el layout para que todo encaje bien
# 5. Mostrar el gráfico
plt.show()
Bibliografía y referencias
- Johnson, R. & Kuby, P. (2008). Estadística elemental: lo esencial (10a ed.). Cengage Learning Editores S.A.