Felipe Maggi.
Lenguaje de programación: Python.
Cuando empezamos algo, lo mejor es hacerlo por el principio. Es necesario asentar bien las bases, para asegurarnos de que entendemos lo que estamos haciendo cuando lleguemos a fases más avanzadas.
Hoy, con la explosión de paquetes y librerías disponibles en R y Python (por nombrar sólo los lenguajes más comunes) útiles para el análisis y la modelización de datos, más el advenimiento de de la IA generativa, que es capaz de escribir código, es muy común ver gente tirándose de cabeza a entrenar modelos, incluyendo redes neuronales, sin tener claros los conceptos básicos de estadística y probabilidad que justifican el uso de un modelo u otro, y que permiten interpretar correctamente los resultados de dichos modelos.
Hagamos honor al primer párrafo, y partamos por lo más básico, definiendo la estadística y algunos conceptos esenciales como población, muestra, parámetro y estadístico.
Para realizar esta labor hay mucha bibliografía disponible, que facilitaremos al final de este artículo, pero en esta ocasión nos guiaremos en parte por lo expuesto en el material del Máster de Big Data & Data Science de la Universidad de Barcelona, por Dolores Lorente porque, a nuestro entender, organiza la materia de forma muy adecuada.
Robert Johnson y Patrica Kuby, en su libro Estadística elemental: lo esencial, definen la estadística como “la ciencia que se encarga de obtener, describir e interpretar los datos” (Jason & Kuby, 2008).
Según los mismos autores, “la estadística puede dividirse en dos grandes campos de acción: estadística descriptiva y estadística inferencial. La estadística descriptiva incluye la obtención, presentación y descripción de los datos muestrales. El término estadística inferencial se refiere a la técnica de interpretación de los valores resultantes de las técnicas descriptivas y la toma de decisiones, así como a la obtención de conclusiones relativas a la población” (ibid).
En el párrafo anterior se han introducido dos conceptos básicos: población y muestra.
La población es, según nuestros autores de referencia, “la colección completa, o conjunto total de individuos, objetos o eventos cuyas propiedades serán analizadas”.
La población puede ser finita o infinita (según si los elementos de la misma se pueden enumerar fácilmente o no). A menudo, aún con poblaciones finitas, el número de elementos es muy grande, por lo que se suele trabajar con una muestra.
Una muestra es un subconjunto de la población, y está constituida por individuos, objetos o elementos seleccionados de la población.
Cuando trabajamos con la población, los valores numéricos que resumen los datos se llaman parámetros. Si estamos trabajando con una muestra, esos mismos valores numéricos se conocen como estadísticos.
Volviendo a Jason & Kuby, una variable “es una característica de interés relacionada con cada elemento individual de una población o muestra”. Parámetros y estadísticos resumen los valores de las variables.
Es importante tener en cuenta que los parámetros tienen un valor fijo, pero no así los estadísticos. Un estadístico puede variar, y de hecho lo hace, cada vez que se selecciona una muestra distinta de la población. Esto, que ahora mencionamos de pasada, es una de las columnas vertebrales de lo que vendrá después.
Un dato “es el valor de la variable asociada a un elemento de la población o muestra. Este valor puede ser un número, una palabra o un símbolo”.
Los datos “son el conjunto de valores que se obtienen de la variable a partir de cada uno de los elementos que pertenecen a la muestra”.
Finalmente, en estadística, un experimento se define como “una actividad planificada cuyos resultados producen un conjunto de datos”.
Por ejemplo, y de forma similar a como nuestros autores de referencia lo exponen, si queremos determinar la nota media obtenida en los exámenes de matemáticas por los estudiantes de segundo de bachillerato del instituto Luis Vives de Valencia, en el año académico 2024-2025… (si alguien lee este post antes de que acabe el 2025, que suponga que ya estamos en el 2026).
- La población será la colección de todas las notas obtenidas en todos los exámenes de matemáticas de todos los alumnos de segundo de bachillerato del instituto Luís Vives, durante el año académico 2024-2025.
- Una muestra será cualquier subconjunto de la población. Por ejemplo, las notas de los exámenes de matemáticas realizados por los alumnos del grupo B de segundo de bachillerato, o las notas de un grupo de alumnos seleccionados de cada grupo.
- La variable es la nota de cada uno de los exámenes.
- Un dato es la nota obtenida por uno de los estudiantes de segundo de bachillerato, en uno de los exámenes de matemáticas del año académico en cuestión.
- Los datos serían el conjunto de notas obtenidas en los exámenes de matemáticas correspondientes a la muestra.
- El experimento es el método aplicado para seleccionar las notas que conforman la muestra. Por ejemplo, preguntando al azar a varios alumnos de segundo de bachillerato qué notas han sacado en sus exámenes de matemáticas.
- El parámetro sobre el que se está buscando información es el valor promedio de todas las notas de la población.
El estadístico que encontrará el experimento es el valor promedio de todas las notas de la muestra.
Antes de continuar, vamos a poner algo de pimienta y sal en este plato para facilitar su digestión (en realidad, para evitar que los lectores abandonen antes del final).
Vamos a hacer un pequeño experimento, consistente en:
- Generar con Python una serie de notas de matemáticas de alumnos de segundo de bachillerato, que será nuestra población, y calcularemos la media de la población. Este será nuestro parámetro.
- De esa población, vamos a seleccionar de forma aleatoria un subconjunto de datos (una muestra), y vamos a calcular la nota media de esa muestra. Este será nuestro estadístico.
- Repetiremos el paso 2 varias veces, seleccionando aleatoriamente datos de la población, y volveremos a calcular la media. Spoiler: las medias serán distintas cada vez, y no serán iguales a las de los pasos anteriores.
- Aunque es adelantarse un poco, graficaremos las medias obtenidas con un tipo de gráfico conocido como de “densidad”. Este último paso lo hacemos para ponerle imágenes al artículo, y para ir adelantando un concepto básico de la estadística que, en gran medida, es el que sostiene todo el edificio, desde los conceptos de población y muestra, hasta las redes neuronales convolucionales (las madres de ChatGPT).
Generación de datos
El siguiente código genera datos simulados de 160 estudiantes (40 estudiantes, por 4 grupos de segundo de bachillerato). En el instituto Luis Vives de Valencia meten caña en matemáticas, y los alumnos han hecho 10 exámenes en el período académico 2024-2025. Por lo tanto, nuestra población (todas las notas), asciende a 1.600 datos.
import pandas as pd
import numpy as np
import random
import string
import seaborn as sns
import matplotlib.pyplot as plt
# --- CONFIGURACIÓN INICIAL ---
np.random.seed(42)
random.seed(42)
def generar_id_estudiante(n):
ids = []
for _ in range(n):
id_estudiante = ''.join(random.choices(
string.ascii_uppercase + string.digits, k=8))
ids.append(id_estudiante)
return ids
# --- PARÁMETROS ---
num_estudiantes_por_grupo = 40
total_estudiantes = num_estudiantes_por_grupo * 4
num_notas = 10
ids = generar_id_estudiante(total_estudiantes)
asignatura = 'Matemáticas'
temas = [f'Tema {i+1}' for i in range(num_notas)] # Tema 1 al 10
fecha_inicio = pd.Timestamp('2024-09-01')
grupos = ['A', 'B', 'C', 'D']
# --- FUNCIÓN para generar correlación entre notas y tiempo de estudio ---
def generar_tiempo_estudio(notas, media=270, sd_total=60, correlacion=0.75):
"""
Genera tiempos de estudio correlacionados con las notas.
"""
# 1. Calcular desviación estándar de las notas actuales
sd_notas = np.std(notas)
if sd_notas == 0: sd_notas = 1 # Evitar división por cero si todas las
# notas son iguales
# 2. Calcular la pendiente (m) necesaria
# Fórmula de regresión: m = r * (Sy / Sx)
pendiente = correlacion * (sd_total / sd_notas)
# 3. Calcular el ruido residual necesario
# Para mantener la SD total deseada, el ruido se reduce si la
# correlación es alta
sd_ruido = sd_total * np.sqrt(1 - correlacion**2)
# 4. Generar ruido y calcular tiempo
ruido = np.random.normal(0, sd_ruido, len(notas))
tiempo_estudio = media + pendiente * (notas - np.mean(notas)) + ruido
return tiempo_estudio.clip(60, 480).astype(int)
# --- GENERACIÓN DE DATOS ---
data = {
'id_estudiante': [], 'asignatura': [], 'tema': [], 'fecha': [],
'nota': [], 'calificacion': [], 'estatura': [], 'sexo': [],
'tiempo_estudio': [], 'grupo': []
}
# Asignar grupos
grupo_asignado = np.repeat(grupos, num_estudiantes_por_grupo)
random.shuffle(grupo_asignado)
for idx, id_estudiante in enumerate(ids):
fechas = [fecha_inicio + pd.DateOffset(weeks=i*4) for i in range(num_notas)]
notas = np.random.normal(6.5, 1, num_notas).clip(0, 10)
estatura = np.random.uniform(150, 190, num_notas)
sexo = random.choice(['H', 'M'])
# Usamos la nueva función (he puesto correlación 0.85 para que
# sea bien visible)
tiempo_estudio = generar_tiempo_estudio(notas, correlacion=0.75)
for i in range(num_notas):
data['id_estudiante'].append(id_estudiante)
data['asignatura'].append(asignatura)
data['tema'].append(temas[i])
data['fecha'].append(fechas[i])
data['nota'].append(round(notas[i], 2))
if 9 <= notas[i] <= 10: calificacion = 'sobresaliente'
elif 7 <= notas[i] < 9: calificacion = 'notable'
elif 5 <= notas[i] < 7: calificacion = 'aprobado'
else: calificacion = 'suspenso'
data['calificacion'].append(calificacion)
data['estatura'].append(estatura[i])
data['sexo'].append(sexo)
data['tiempo_estudio'].append(tiempo_estudio[i])
data['grupo'].append(grupo_asignado[idx])
df = pd.DataFrame(data)
df['aprobado'] = df['calificacion'].apply(lambda x: 0 if x == 'suspenso' else 1)
# Asegurar orden correcto de temas
orden_temas = [f'Tema {i}' for i in range(1, 11)]
df['tema'] = pd.Categorical(df['tema'], categories=orden_temas, ordered=True)
# Mostrar el DataFrame
print(df)
id_estudiante asignatura tema fecha nota calificacion \
0 XAJI0Y6D Matemáticas Tema 1 2024-09-01 7.00 aprobado
1 XAJI0Y6D Matemáticas Tema 2 2024-09-29 6.36 aprobado
2 XAJI0Y6D Matemáticas Tema 3 2024-10-27 7.15 notable
3 XAJI0Y6D Matemáticas Tema 4 2024-11-24 8.02 notable
4 XAJI0Y6D Matemáticas Tema 5 2024-12-22 6.27 aprobado
... ... ... ... ... ... ...
1595 FNKOMV2X Matemáticas Tema 6 2025-01-19 7.28 notable
1596 FNKOMV2X Matemáticas Tema 7 2025-02-16 6.48 aprobado
1597 FNKOMV2X Matemáticas Tema 8 2025-03-16 7.70 notable
1598 FNKOMV2X Matemáticas Tema 9 2025-04-13 5.40 aprobado
1599 FNKOMV2X Matemáticas Tema 10 2025-05-11 3.32 suspenso
estatura sexo tiempo_estudio grupo
0 165.365823 H 357 C
1 165.342702 H 256 C
2 172.419623 H 274 C
3 150.867198 H 185 C
4 152.750822 H 236 C
... ... ... ... ...
1595 166.943894 M 195 A
1596 177.309590 M 299 A
1597 163.493402 M 154 A
1598 150.000000 M 146 A
1599 168.297418 M 312 A
[1600 rows x 10 columns]
Definición del experimento
A final de año académico 2024-2025, el responsable de orientación escolar le ha pedido a un grupo de alumnos que calcule la nota media de los exámenes de matemáticas.
Los alumnos no tienen acceso a la tabla anterior, por lo que tienen que averiguar, de alguna forma, las notas en cuestión. Pero estamos hablando de 1.600 notas. Aunque pudieran entrevistar a todos los alumnos (160), y preguntarles por sus notas en cada uno de los exámenes, no llegarían a tiempo para entregar el trabajo (les han dado una semana de plazo). Por lo tanto, deciden trabajar con una muestra aleatoria.
Le preguntan al profesor de mates, y éste les recomienda el número mínimo de notas a recolectar, y la forma de seleccionarlas.
Al final, van a trabajar con 40 notas (10 notas por grupo), y para recolectarlas van a hacer lo siguiente:
- En cada grupo, le pedirán a un alumno que saque 10 papeletas de una cesta que contiene 40 papeletas con los nombres de cada estudiante del grupo correspondiente. No hace falta devolver la papeleta a la cesta entre extracción y extracción, con lo que se aseguran de que están eligiendo a 10 alumnos distintos por grupo. Es lo que se conoce como muestreo aleatorio simple sin reemplazo.
- En otra cesta, meterán 10 papeletas con los temas de los exámenes (tema 1, tema 2, tema 3…), y le pedirán a cada uno de los alumnos seleccionados en el paso 1 que saque una papeleta, diga el tema que le ha tocado, y la nota que obtuvo en ese examen, y que luego devuelva la papeleta a la cesta. Es decir, es posible que dentro de un grupo se repita un tema. Esto se llama muestreo aleatorio simple con reemplazo.
- Los pasos 1 y 2 se repiten en cada uno de los 4 grupos.
Damos tantos detalles porque la forma de recolectar las notas es muy importante. La selección debe ser lo más aleatoria posible para evitar sesgos. Por ejemplo: recolectar todas las notas en un grupo que tiene problemas con las mates, y cuya nota media es menor que el resto. O preguntarles a todos por la nota en el examen de un mismo tema, que era muy sencillo.
Sería como hacer una encuesta sobre la intención de voto sólo en el barrio de Almagro, o sólo en el de Lavapiés, en Madrid.
Evidentemente, el responsable de orientación escolar sabe la nota media de la población, porque tiene acceso a las actas de notas de todo el instituto. Vamos a calcularla:
# Calcular la media de la columna nota
media_nota = round(df['nota'].mean(), 2)
print(f"La media de la columna 'nota' es: {media_nota}")
La media de la columna 'nota' es: 6.49
La nota media ronda el 6.5 Este es nuestro parámetro. Vamos a ver qué estadístico sacamos de la muestra.
Para ello, vamos pedirle a Python que simule el experimento descrito.
Experimento 1
# Lista de grupos
grupos = df['grupo'].unique()
# Seleccionar al azar 10 alumnos de cada grupo (sin reemplazo)
alumnos_muestra = []
for grupo in grupos:
alumnos_grupo = df[df['grupo'] == grupo]['id_estudiante'].unique()
muestra_grupo = random.sample(list(alumnos_grupo), 10)
alumnos_muestra.extend(muestra_grupo)
# Seleccionar al azar un tema para cada alumno de la muestra (con reemplazo)
temas_muestra = {}
for alumno in alumnos_muestra:
notas_alumno = df[df['id_estudiante'] == alumno]
tema_elegido = random.choice(notas_alumno['tema'].unique())
temas_muestra[alumno] = tema_elegido
# Crear el DataFrame de muestra con los temas seleccionados
dfs_alumnos_temas = []
for alumno, tema in temas_muestra.items():
df_alumno_tema = df[(df['id_estudiante'] == alumno) & (df['tema'] == tema)]
dfs_alumnos_temas.append(df_alumno_tema)
df_muestra_1 = pd.concat(dfs_alumnos_temas, ignore_index=True)
# Calcular la nota media de la muestra
nota_media_muestra_1 = df_muestra_1['nota'].mean()
# Mostrar el DataFrame de muestra y la nota media
print("DataFrame de muestra:")
print(df_muestra_1.head())
print()
print(f"Nota media de la muestra: {nota_media_muestra_1:.2f}")
DataFrame de muestra:
id_estudiante asignatura tema fecha nota calificacion \
0 PKYRYBOV Matemáticas Tema 9 2025-04-13 7.09 notable
1 GNZS43C5 Matemáticas Tema 5 2024-12-22 6.70 aprobado
2 1V2ISQP4 Matemáticas Tema 2 2024-09-29 5.81 aprobado
3 JUY0BVR6 Matemáticas Tema 5 2024-12-22 8.47 notable
4 MZSGIPPS Matemáticas Tema 4 2024-11-24 6.91 aprobado
estatura sexo tiempo_estudio grupo
0 163.275144 M 288 C
1 160.994096 M 237 C
2 179.681847 M 302 C
3 174.359754 M 238 C
4 165.931148 H 293 C
Nota media de la muestra: 6.38
Los alumos han llevado a cabo el experimento, y obtienen una media algo distinta a la media «real», pero se acerca bastante.
A tener en cuenta: ellos no conocen la media de la población.
El profesor les da una semana más, y les pide que repitan el experimento 4 veces más. Los alumnos, a parte de cabrearse, se ponen manos a la obra.
Experimento 2
# Lista de grupos
grupos = df['grupo'].unique()
# Seleccionar al azar 10 alumnos de cada grupo (sin reemplazo)
alumnos_muestra = []
for grupo in grupos:
alumnos_grupo = df[df['grupo'] == grupo]['id_estudiante'].unique()
muestra_grupo = random.sample(list(alumnos_grupo), 10)
alumnos_muestra.extend(muestra_grupo)
# Seleccionar al azar un tema para cada alumno de la muestra (con reemplazo)
temas_muestra = {}
for alumno in alumnos_muestra:
notas_alumno = df[df['id_estudiante'] == alumno]
tema_elegido = random.choice(notas_alumno['tema'].unique())
temas_muestra[alumno] = tema_elegido
# Crear el DataFrame de muestra con los temas seleccionados
dfs_alumnos_temas = []
for alumno, tema in temas_muestra.items():
df_alumno_tema = df[(df['id_estudiante'] == alumno) & (df['tema'] == tema)]
dfs_alumnos_temas.append(df_alumno_tema)
df_muestra_2 = pd.concat(dfs_alumnos_temas, ignore_index=True)
# Calcular la nota media de la muestra
nota_media_muestra_2 = df_muestra_2['nota'].mean()
# Mostrar el DataFrame de muestra y la nota media
print("DataFrame de muestra:")
print(df_muestra_2.head())
print()
print(f"Nota media de la muestra: {nota_media_muestra_2:.2f}")
DataFrame de muestra:
id_estudiante asignatura tema fecha nota calificacion \
0 PNSM43D8 Matemáticas Tema 3 2024-10-27 5.63 aprobado
1 JUY0BVR6 Matemáticas Tema 8 2025-03-16 7.99 notable
2 PSEIMVIH Matemáticas Tema 9 2025-04-13 5.02 aprobado
3 9T84AZYT Matemáticas Tema 8 2025-03-16 6.51 aprobado
4 X7EEDTJV Matemáticas Tema 8 2025-03-16 6.62 aprobado
estatura sexo tiempo_estudio grupo
0 170.409192 M 268 C
1 171.261779 M 283 C
2 178.303358 H 242 C
3 171.833420 M 382 C
4 155.356251 H 175 C
Nota media de la muestra: 6.36
Experimento 3
# Lista de grupos
grupos = df['grupo'].unique()
# Seleccionar al azar 10 alumnos de cada grupo (sin reemplazo)
alumnos_muestra = []
for grupo in grupos:
alumnos_grupo = df[df['grupo'] == grupo]['id_estudiante'].unique()
muestra_grupo = random.sample(list(alumnos_grupo), 10)
alumnos_muestra.extend(muestra_grupo)
# Seleccionar al azar un tema para cada alumno de la muestra (con reemplazo)
temas_muestra = {}
for alumno in alumnos_muestra:
notas_alumno = df[df['id_estudiante'] == alumno]
tema_elegido = random.choice(notas_alumno['tema'].unique())
temas_muestra[alumno] = tema_elegido
# Crear el DataFrame de muestra con los temas seleccionados
dfs_alumnos_temas = []
for alumno, tema in temas_muestra.items():
df_alumno_tema = df[(df['id_estudiante'] == alumno) & (df['tema'] == tema)]
dfs_alumnos_temas.append(df_alumno_tema)
df_muestra_3 = pd.concat(dfs_alumnos_temas, ignore_index=True)
# Calcular la nota media de la muestra
nota_media_muestra_3 = df_muestra_3['nota'].mean()
# Mostrar el DataFrame de muestra y la nota media
print("DataFrame de muestra:")
print(df_muestra_3.head())
print()
print(f"Nota media de la muestra: {nota_media_muestra_3:.2f}")
DataFrame de muestra:
id_estudiante asignatura tema fecha nota calificacion \
0 1N13JCAT Matemáticas Tema 10 2025-05-11 8.46 notable
1 PSEIMVIH Matemáticas Tema 5 2024-12-22 7.33 notable
2 7SRCBPLJ Matemáticas Tema 8 2025-03-16 4.94 suspenso
3 VDZ4X1ZH Matemáticas Tema 1 2024-09-01 8.67 notable
4 B2KNFTU2 Matemáticas Tema 6 2025-01-19 7.27 notable
estatura sexo tiempo_estudio grupo
0 170.979832 M 268 C
1 171.818663 H 332 C
2 154.644279 M 190 C
3 178.622235 M 283 C
4 171.480894 M 386 C
Nota media de la muestra: 6.75
Experimento 4
# Lista de grupos
grupos = df['grupo'].unique()
# Seleccionar al azar 10 alumnos de cada grupo (sin reemplazo)
alumnos_muestra = []
for grupo in grupos:
alumnos_grupo = df[df['grupo'] == grupo]['id_estudiante'].unique()
muestra_grupo = random.sample(list(alumnos_grupo), 10)
alumnos_muestra.extend(muestra_grupo)
# Seleccionar al azar un tema para cada alumno de la muestra (con reemplazo)
temas_muestra = {}
for alumno in alumnos_muestra:
notas_alumno = df[df['id_estudiante'] == alumno]
tema_elegido = random.choice(notas_alumno['tema'].unique())
temas_muestra[alumno] = tema_elegido
# Crear el DataFrame de muestra con los temas seleccionados
dfs_alumnos_temas = []
for alumno, tema in temas_muestra.items():
df_alumno_tema = df[(df['id_estudiante'] == alumno) & (df['tema'] == tema)]
dfs_alumnos_temas.append(df_alumno_tema)
df_muestra_4 = pd.concat(dfs_alumnos_temas, ignore_index=True)
# Calcular la nota media de la muestra
nota_media_muestra_4 = df_muestra_4['nota'].mean()
# Mostrar el DataFrame de muestra y la nota media
print("DataFrame de muestra:")
print(df_muestra_4.head())
print()
print(f"Nota media de la muestra: {nota_media_muestra_4:.2f}")
DataFrame de muestra:
id_estudiante asignatura tema fecha nota calificacion \
0 K2VMWWYZ Matemáticas Tema 3 2024-10-27 6.93 aprobado
1 9T84AZYT Matemáticas Tema 5 2024-12-22 7.19 notable
2 UZFK8UT0 Matemáticas Tema 1 2024-09-01 6.31 aprobado
3 NF7C3DD0 Matemáticas Tema 5 2024-12-22 7.81 notable
4 ID25OWF7 Matemáticas Tema 2 2024-09-29 6.78 aprobado
estatura sexo tiempo_estudio grupo
0 175.222506 M 278 C
1 190.000000 M 224 C
2 164.827115 M 188 C
3 182.347519 H 267 C
4 183.920023 M 190 C
Nota media de la muestra: 6.31
Experimento 5
# Lista de grupos
grupos = df['grupo'].unique()
# Seleccionar al azar 10 alumnos de cada grupo (sin reemplazo)
alumnos_muestra = []
for grupo in grupos:
alumnos_grupo = df[df['grupo'] == grupo]['id_estudiante'].unique()
muestra_grupo = random.sample(list(alumnos_grupo), 10)
alumnos_muestra.extend(muestra_grupo)
# Seleccionar al azar un tema para cada alumno de la muestra (con reemplazo)
temas_muestra = {}
for alumno in alumnos_muestra:
notas_alumno = df[df['id_estudiante'] == alumno]
tema_elegido = random.choice(notas_alumno['tema'].unique())
temas_muestra[alumno] = tema_elegido
# Crear el DataFrame de muestra con los temas seleccionados
dfs_alumnos_temas = []
for alumno, tema in temas_muestra.items():
df_alumno_tema = df[(df['id_estudiante'] == alumno) & (df['tema'] == tema)]
dfs_alumnos_temas.append(df_alumno_tema)
df_muestra_5 = pd.concat(dfs_alumnos_temas, ignore_index=True)
# Calcular la nota media de la muestra
nota_media_muestra_5 = df_muestra_5['nota'].mean()
# Mostrar el DataFrame de muestra y la nota media
print("DataFrame de muestra:")
print(df_muestra_5.head())
print()
print(f"Nota media de la muestra: {nota_media_muestra_5:.2f}")
DataFrame de muestra:
id_estudiante asignatura tema fecha nota calificacion \
0 TRP0J43D Matemáticas Tema 3 2024-10-27 7.00 aprobado
1 1N13JCAT Matemáticas Tema 1 2024-09-01 4.52 suspenso
2 9T84AZYT Matemáticas Tema 6 2025-01-19 6.10 aprobado
3 OM5IGQPK Matemáticas Tema 5 2024-12-22 7.09 notable
4 253J2D54 Matemáticas Tema 10 2025-05-11 8.13 notable
estatura sexo tiempo_estudio grupo
0 166.801525 M 259 C
1 157.704504 M 287 C
2 162.326524 M 278 C
3 154.433708 M 268 C
4 154.441044 H 267 C
Nota media de la muestra: 6.73
Los alumnos se dan cuenta de que cada vez que realizan el experimento, obtienen una media distinta. Uno de ellos se pregunta entonces cómo pueden estar seguros de la media de la población… Ya llegaremos ahí. Este es un viaje de largo recorrido. Una carrera de fondo.
Advertencia: si se ejecutan los códigos de los experimentos del 1 al 5, las medias arrojadas cambiarán cada vez.
Distribuciones de datos
Para poner algo de color, a continuación mostraremos la distribución de las notas, tanto de la población, como de una de las muestras, y luego compararemos esas distribuciones.
Esto es adelantarse un poco, pero es interesante ir asomándose a cosas que vendrán después. Aquí, como ejercicio, es conveniente observar las distribuciones y pensar qué nos están diciendo.
Población
import seaborn as sns
import matplotlib.pyplot as plt
# Graficar la densidad de las notas usando Seaborn (población=
plt.figure(figsize=(10, 6))
sns.kdeplot(data=df['nota'], fill=True, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Densidad')
plt.show()
Muestra 5
# Graficar la densidad de las notas usando Seaborn (muestra 5)
plt.figure(figsize=(10, 6))
sns.kdeplot(data=df_muestra_5['nota'], fill=True, color='red')
plt.title('Distribución de Notas de la Muestra 5')
plt.xlabel('Nota')
plt.ylabel('Densidad')
plt.show()
Las notas de la muestra 5 tienen una media distinta, como es de esperar, pero también una distribución ligeramente diferente.
Advertencia: insisto, si se ejecutan estos códigos, las medias y las distribuciones cambiarán.
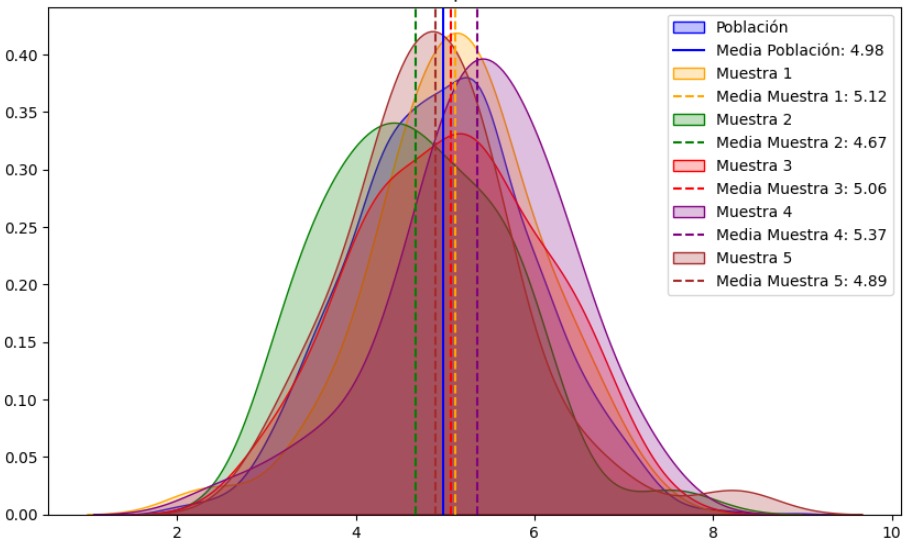
Como último atisbo a lo que hay detrás de todo esto, vamos a observar cómo se distribuyen las notas de las distintas muestras, junto con la original. ¿Qué conclusiones sugiere el gráfico?
# Lista de DataFrames y etiquetas
dataframes = [df, df_muestra_1, df_muestra_2, df_muestra_3, df_muestra_4, df_muestra_5]
labels = ['Población', 'Muestra 1', 'Muestra 2', 'Muestra 3', 'Muestra 4', 'Muestra 5']
# Colores específicos para cada muestra
colors = ['blue', 'orange', 'green', 'red', 'purple', 'brown']
# Configuración del gráfico
plt.figure(figsize=(10, 6))
# Graficar densidad de notas para cada DataFrame
for i, df_temp in enumerate(dataframes):
# Determinar color y estilo de la línea vertical
color = colors[i]
linestyle = '-' if i == 0 else '--'
# Graficar densidad de notas
sns.kdeplot(data=df_temp['nota'], label=labels[i], fill=True, color=color)
# Calcular y graficar la media como línea vertical punteada
mean_nota = df_temp['nota'].mean()
plt.axvline(x=mean_nota, linestyle=linestyle, color=color, label=f'Media {labels[i]}: {mean_nota:.2f}')
plt.title('Distribución de Notas por Muestra con Medias')
plt.xlabel('Nota')
plt.ylabel('Densidad')
plt.legend()
plt.show()
La línea azul continua representa la media de la población. Las líneas discontinuas son las medias de las muestras.
Esto es un ejemplo del hecho que comentábamos antes, y que recordamos de nuevo aquí: un estadístico puede variar, y de hecho lo hace, cada vez que se selecciona una muestra distinta de la población, pero el parámetro de la población permanece fijo.
No hay que olvidarse nunca de esto.
Tipos de variables
A continuación vamos tratar otro tema muy importante, al que se le suele prestar poca atención, pero que es esencial para pisar en terreno firme: los tipos de variables estadísticas.
En el campo que nos ocupa hay dos tipos fundamentales de variables: las que aportan información cualitativa, y las que aportan información cuantitativa.
Según, de nuevo, Johnson y Kuby, una variable cualitativa, de atributos o categórica, «es una variable que clasifica o describe a un elemento de una población«.
Una variable cuantitativa o numérica es aquella que «cuantifica un elemento de una población«.
Es un error común definir a las variables numéricas diciendo que son aquellas cuyo valor es un número. Las variables numéricas son aquellas que tiene sentido sumar y promediar.
Los códigos postales o los IDs, por ejemplo, suelen ser números, pero no son variables numéricas. Los años también son números, pero tampoco son variables numéricas. No tiene sentido promediar códigos postales, o IDs. Tampoco se suele coger una lista de años, para sacar el promedio de esa lista.
¿Alguna vez ha visto algún estudio en el que se diga que el año promedio en que pasaron las cosas fue en 2022.5, que es lo que sale de promediar los años 2021, 2022, 2023 y 2024?
¿O algún análisis en los que la suma de los años como tales tenga relevancia? De cara sacar información de un conjunto de datos, ¿nos sirve de algo saber que 2021, 2022, 2023 y 2024 suman 8.090?
Variables cualitativas
Dentro de las variables cualitativas o categóricas, nos encontramos con variables:
- Nominales
- Ordinales
Según Johnson y Kuby, podemos definir cada tipo de la siguiente manera:
Variable nominal
Una variable nominal «es una variable cualitativa que caracteriza (describe o identifica) a un elemento de una población. Para los datos resultantes de una variable nominal, las operaciones aritméticas no sólo carecen de sentido, sino que tampoco se puede asignar un orden a las categorías«.
Como ejemplos de variables nominales podemos poner el color de ojos, o de pelo. La cuidad de residencia, el sexo, el género de una película, el estado civil, la condición de fumador o no fumador, o de estado de salud (enfermo o sano).
Variable nominal dicotómica
Una variable nominal, además, puede o no ser dicotómica. Las variables nominales dicotómicas son aquellas que sólo adoptan dos valores posibles (sí o no, 0 ó 1). En los ejemplos anteriores, el sexo (hombre o mujer), se suele tratar como dicotómica (aunque es posible encontrar cojuntos de datos en los que hay más de dos valores (hombre, mujer, no-binario). En ese caso la variable no es dicotómica.
El estado civil podría serlo, si en el conjunto de datos analizado sólo adopta los valores de casado o soltero.
Finalmente, si el estado de salud adopta los valores de enfermo o sano, también sería dicotómica.
Variable ordinal
Por su parte, una variable ordinal «es una variable cualitativa que presenta una posición, o clasificación, ordenada«.
Un ejemplo de variable ordinal puede ser la valoración que se le da a una película, en una escala de 1 a 5 (aunque según qué casos es posible tratar dicha valoración como una variable numérica).
Otro ejemplo, quizá más claro, es la clasificación con letras de un determinado elemento. Por ejemplo, una habitación clasificada con las letras A, B y C según la calidad de la habitación (o con las palabras «lujo», normal, «barata»). En orden de calidad creciente, «barata» va antes que «normal», y «normal» antes que «lujo».
Representación gráfica
En general, cuando queremos representar variables cualitativas se utilizan gráficos de barras. En uno de los ejes se muestran los valores que toma la variable, y en el otro la frecuencia con la que aparece dicho valor en el conjunto de datos. Las barras adoptan una altura proporcional a dicha frecuencia (si se quiere saber más sobre frecuencias de datos, recomendamos leer el segundo artículo de esta serie).
El siguiente gráfico muestra el número total (la frecuencia absoluta) de suspensos, aprobados y notables que hay en el conjunto de datos con las notas de matemáticas.
import matplotlib.pyplot as plt
# Contar las ocurrencias de cada calificación
conteo_calificaciones = df['calificacion'].value_counts()
# Crear el gráfico de barras
plt.figure(figsize=(8, 6))
barras = conteo_calificaciones.plot(kind='bar', color='skyblue')
# Añadir título y etiquetas
plt.title('Frecuencia de Calificaciones', fontsize=12)
plt.xlabel('Calificación', fontsize=10)
plt.ylabel('Cantidad de Estudiantes', fontsize=10)
# Añadir los valores de conteo dentro de cada barra
for i in barras.containers:
barras.bar_label(i, labels=[f'{v}' for v in conteo_calificaciones], label_type='edge', fontsize=10)
# Mostrar gráfico
plt.show()
Una forma alternativa es presentar la frecuencia relativa (es decir, el porcentaje de veces que la variable adquiere determinado valor):
import matplotlib.pyplot as plt
# Calcular la frecuencia relativa de cada calificación
frecuencia_relativa = df['calificacion'].value_counts(normalize=True)
# Crear el gráfico de barras con frecuencia relativa
plt.figure(figsize=(8, 6))
barras = frecuencia_relativa.plot(kind='bar', color='skyblue')
# Añadir título y etiquetas
plt.title('Distribución Relativa de Calificaciones', fontsize=12)
plt.xlabel('Calificación', fontsize=10)
plt.ylabel('Frecuencia Relativa', fontsize=10)
# Añadir los valores de frecuencia relativa dentro de cada barra
for i in barras.containers:
barras.bar_label(i, labels=[f'{v:.1%}' for v in frecuencia_relativa], label_type='edge', fontsize=10)
# Mostrar gráfico
plt.show()
Es frecuente utilizar gráficos de sectores (o de tartas) para mostrar esta misma información.
import matplotlib.pyplot as plt
# Calcular la frecuencia relativa de cada calificación
frecuencia_relativa = df['calificacion'].value_counts(normalize=True)
# Crear el gráfico de tarta
plt.figure(figsize=(5, 5))
plt.pie(frecuencia_relativa, labels=frecuencia_relativa.index, autopct='%1.1f%%', colors=plt.cm.Paired.colors)
# Añadir título
plt.title('Distribución de Calificaciones', fontsize=12)
# Mostrar gráfico
plt.show()
No me gustan nada los gráficos de tarta, y no los recomiendo. Aprovecharé, eso sí para advertir lo siguiente: cuando la variable cualitativa adquiere más de seis valores distintos, los gráficos de tarta no son una buena opción. En ese caso, las barras son siempre la elección correcta.
Variables numéricas
Las variables cuantitativas o numéricas se subdividen en:
- Discretas
- Continuas
Johnson y Kuby definen cada tipo de variable numérica de esta forma:
Variable discreta
Una variable discreta es «una variable cuantitativa que puede asumir un número contable (o finito) de valores. Intuitivamente, una variable discreta puede asumir los valores correspondientes a puntos aislados a lo largo de un intervalo de recta. Es decir, entre dos valores cualesquiera siempre hay un hueco.
Esto último es importante: «…entre dos valores cualesquiera siempre hay un hueco. Quedémonos con esto para más adelante.
Un ejemplo de variable discreta es el número de hijos que tiene una pareja: 1, 2, 3, 4… No es posible tener 3.254893 hijos.
Representación gráfica de variables discretas
Histogramas
Una variable discreta también se puede representar con gráficos de barras, aunque lo normal es representarlas mediante histogramas, sobre todo si adquieren un elevado número de valores. Los histogramas son similares a los gráficos de barras, con la salvedad de que las barras no están separadas entre sí.
El ancho de cada barra (denominada también como «contenedor») representa el intervalo de valores incluidos en cada contenedor. La altura de cada barra, o contenedor, es proporcional al número de datos incluidos dentro del mismo.
El siguiente gráfico muestra la distribución de las notas de nuestro conjunto de datos:
# Definir los bordes de los bins
bins = np.linspace(0, 10, 21) # 21 porque queremos 20 intervalos
# Imprimir los bordes de los bins
print("Bordes de los bins:", bins)
# Graficar el histograma de las notas usando Seaborn
plt.figure(figsize=(10, 6))
sns.histplot(data=df['nota'], bins=bins, kde=False, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.show()
Bordes de los bins: [ 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. 7.5 8. 8.5 9. 9.5 10. ]
En este caso concreto, cada barra tiene el mismo ancho, y los límites de los contenedores son [0, 0.5, 1, 1.5, 2, 2.5, 3…]. Es decir, el primer contenedor tiene las notas entre [0, 0.5). El primer valor está incluido en el intervalo, y el segundo no (de ahí los paréntesis distintos). El segundo contenedor tiene las notas entre [0.5, 1), y así sucesivamente.
Como puede verse, no hay notas entre el 0 y el 3, por lo que no hay barras en ese intervalo. Esta visualización no es óptima. En el siguiente artículo mostraremos la manera de seleccionar correctamente el número de contenedores, para este tipo de visualizaciones.
En ocasiones es conveniente trabajar con contenedores de ancho variable, pero eso lo veremos si se da la ocasión.
Diagrama de Frecuencias Acumuladas
Para las variables discretas, o discretizadas, también se suele utilizar el Diagrama de Frecuencias Acumuladas. El siguiente código discretiza las notas redondeándolas a enteros, y muestra el diagrama.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Redondear las notas hacia el entero más cercano
df['nota_discretizada'] = np.round(df['nota']).astype(int)
# Definir los límites de los bins
bins = np.arange(1, 12, 1) # Limites [1, 2, ..., 11] para incluir el 10 redondeado
# Calcular las frecuencias relativas y acumuladas para las notas discretizadas
frecuencia_relativa_notas = df['nota_discretizada'].value_counts(normalize=True).sort_index()
frecuencia_acumulada_notas = frecuencia_relativa_notas.cumsum()
# Crear el diagrama de frecuencias acumuladas sin líneas verticales
plt.figure(figsize=(8, 6))
# Dibujar las líneas horizontales de frecuencias acumuladas con saltos de alturas distintas
for i in range(1, len(frecuencia_acumulada_notas)):
plt.hlines(frecuencia_acumulada_notas.iloc[i-1], i, i+1, colors='blue')
# Añadir la última línea horizontal
plt.hlines(frecuencia_acumulada_notas.iloc[-1], len(frecuencia_acumulada_notas), len(frecuencia_acumulada_notas) + 1, colors='blue')
# Añadir puntos en el extremo izquierdo de cada línea
x_points = np.arange(1, len(frecuencia_acumulada_notas) + 1)
y_points = frecuencia_acumulada_notas.values
plt.scatter(x_points, y_points, color='blue', s=25, marker='o', zorder=5) # Tamaño de los puntos reducido
# Etiquetas en el eje X
plt.xticks(range(len(frecuencia_acumulada_notas)), frecuencia_acumulada_notas.index.astype(str), rotation=45)
# Añadir título y etiquetas
plt.title('Diagrama de Frecuencias Relativas Acumuladas (Notas Discretizadas)', fontsize=12)
plt.xlabel('Notas Discretizadas', fontsize=10)
plt.ylabel('$F_i$ = Frecuencia Relativa Acumulada', fontsize=10)
plt.grid(True)
# Mostrar gráfico
plt.tight_layout()
plt.show()
De nuevo, remitimos al segundo artículo de esta serie para saber más sobre tablas de frecuencias.
Aquí, nos limitaremos a decir que la altura de cada barra indica el porcentaje de notas son iguales o inferiores a un valor concreto. Como los datos son discretos, vemos saltos o escalones. El punto en el extremo izquierdo de cada barra indica que el valor inferior de cada intervalo está incluido en él. El valor superior no, puesto que pertenece al intervalo siguiente.
Este gráfico nos dice, por ejemplo, que cerca del 50% de las notas son iguales o inferiores a 7. La altura en la que se encuentra la barra, por tanto, es proporcional al porcentaje de valores que son iguales o inferiores al valor que marca el punto.
El tamaño de los saltos por su parte, es proporcional a la diferencia de porcentaje entre un valor y otro. Por ejemplo, entre el 7 y el 10, la diferencia es de un 50% (pasamos del 50% al 100% de los datos).
Variable continua
Una variable continua, por su parte, «es una variable cuantitativa que puede asumir una cantidad incontable de valores. Intuitivamente, una variable continua puede asumir cualquier valor a lo largo de un intervalo de recta, incluyendo cualquier valor posible entre dos variables determinadas«.
Es decir no hay huecos en el intervalo analizado.
Como ejemplos de variables continuas, podemos poner la estatura y el peso de una persona. Aunque la persona más bajita del mundo mida 62 centímetros, y la más alta mida 251 centímetros, dentro de ese intervalo podemos encontrarnos con cualquier número si empezamos a medir gente. La cantidad de números dentro de ese intervalo es infinita.
Es común leer, u oír, aquello de que una variable continua es aquella que tiene decimales, pero si los valores que asume la variable son, por ejemplo, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5… y así sucesivamente, la variable es discreta. Aumenta en saltos de 0.5, y entremedio no hay otros valores. Los decimales no garantizan que la variable sea continua.
Representación gráfica de variables continuas
Las variables continuas también se pueden representar mediante histogramas, siempre que las discreticemos antes en contenedores, tal y como hemos hecho con las notas anteriormente.
Sin embargo, es frecuente utilizar los gráficos de densidad, como los que ya hemos visto en el apartado sobre las distribuciones de datos. A continuación mostramos la distribución de estaturas de los alumnos de segundo de bachillerato:
import seaborn as sns
import matplotlib.pyplot as plt
# Graficar la densidad de las estaturas usando Seaborn
plt.figure(figsize=(10, 6))
sns.kdeplot(data=df['estatura'], fill=True, color='blue')
plt.title('Distribución de estaturas')
plt.xlabel('Estatura')
plt.ylabel('Densidad')
plt.show()
En general, toda variable numérica puede ser representada con histogramas y mediante gráficos de frecuencia acumulada. Existen otras visualizaciones, como los gráficos de Boxplot y sus distintas versiones, pero los revisaremos tras haber estudiado antes las medidas de posición.
Análisis de las variables del dataset de notas
Para cerrar, hagamos el ejercicio de analizar el tipo de variables que tienen nuestro conjunto de datos con las notas de matemáticas. En Python, la función .info() nos da la lista de variables y la tipificación de las mismas… Pero cuidado, esa tipificación no es la hemos estado repasando hasta ahora (en R podemos usar la función .str)
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 1600 entries, 0 to 1599 Data columns (total 11 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 id_estudiante 1600 non-null object 1 asignatura 1600 non-null object 2 tema 1600 non-null object 3 fecha 1600 non-null datetime64[ns] 4 nota 1600 non-null float64 5 calificacion 1600 non-null object 6 estatura 1600 non-null float64 7 sexo 1600 non-null object 8 tiempo_estudio 1600 non-null int64 9 grupo 1600 non-null object 10 nota_discretizada 1600 non-null int64 dtypes: datetime64[ns](1), float64(2), int64(2), object(6) memory usage: 137.6+ KB
Como podemos ver, en la columna Dtype, Python nos dice que la variable id_estudiante es un «object», que fecha es «datetime64[ns]», que nota es «float», que tiempo de estudio es «int64». etc…
Esto es útil en cierta medida, porque en principio las variables tipo «object» serán cualitativas, y las de tipo «int64» y «float64» serán numéricas. Pero hasta aquí llega la ayuda.
Para determinar la verdadera naturaleza de las variables, más allá de esto, es necesario estudiar nuestro conjunto de datos en profundidad.
Podría pasar, por ejemplo, que tuviéramos otra variable, que fuera «aprobado», y que en el dataframe se haya codificado como 1, en los casos en los que el alumno ha aprobado el examen, y como 0, si ha suspendido. En ese caso, Python, en su inocencia, nos dirá que la variable es «Int64». Pero en realidad es una variable nominal dicotómica.
Vamos a comprobarlo. Vamos a añadir a nuestro dataframe con las notas la columna «aprobado», asignando un 1 si la calificación es distinta de «suspenso», y un 0, si es igual a «suspenso».
# Añadir la columna "aprobado"
df['aprobado'] = df['calificacion'].apply(lambda x: 0 if x == 'suspenso' else 1)
# Mostrar el DataFrame con la nueva columna "aprobado"
print(df.head())
id_estudiante asignatura tema fecha nota calificacion \
0 XAJI0Y6D Matemáticas Tema 1 2024-09-01 7.00 aprobado
1 XAJI0Y6D Matemáticas Tema 2 2024-09-29 6.36 aprobado
2 XAJI0Y6D Matemáticas Tema 3 2024-10-27 7.15 notable
3 XAJI0Y6D Matemáticas Tema 4 2024-11-24 8.02 notable
4 XAJI0Y6D Matemáticas Tema 5 2024-12-22 6.27 aprobado
estatura sexo tiempo_estudio grupo nota_discretizada aprobado
0 165.365823 H 357 C 7 1
1 165.342702 H 256 C 6 1
2 172.419623 H 274 C 7 1
3 150.867198 H 185 C 8 1
4 152.750822 H 236 C 6 1
Si ahora le preguntamos a Python, ya sabemos lo que va a pasar:
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 1600 entries, 0 to 1599 Data columns (total 12 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 id_estudiante 1600 non-null object 1 asignatura 1600 non-null object 2 tema 1600 non-null object 3 fecha 1600 non-null datetime64[ns] 4 nota 1600 non-null float64 5 calificacion 1600 non-null object 6 estatura 1600 non-null float64 7 sexo 1600 non-null object 8 tiempo_estudio 1600 non-null int64 9 grupo 1600 non-null object 10 nota_discretizada 1600 non-null int64 11 aprobado 1600 non-null int64 dtypes: datetime64[ns](1), float64(2), int64(3), object(6) memory usage: 150.1+ KB
La nueva columna tiene como Dtype «int64», pero como ya dijimos, es una variable nominal dicotómica que indica si el alumno o alumna ha aprobado o no, (con 1 y 0, respectivamente).
Así que pongámonos manos a la obra, y revisemos variable por variable.
Antes de continuar, debemos explicar una cosa: en este caso, en el que hemos creado un dataframe de ejemplo, conocemos la naturaleza de cada variable de antemano, y el tipo de valores que contienen. En la vida real, esto no es así. Lo normal es que nos encontremos con conjunto de datos, de miles o millones de líneas y quizá cientos de variables, de las que NO SABEMOS NADA, más allá de una descripción somera.
id_estudiante
# Muestra de 5 valores al azar de la variable id_estudiante
random_sample = df['id_estudiante'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
1253 DYT9MOGE 482 OKEP7Y6W 1113 MVXPJ4HN 188 PHT0HL9X 1307 0S0R2SDS Name: id_estudiante, dtype: object
Hemos seleccionado 5 valores elegidos al azar. Podemos ver más si cambiamos .sample(5) por .sample(10), o por el valor que queramos.
Como puede verse, se trata de valores alfanuméricos, que identifican a cada estudiante.
Es una variable cualitativa o categórica nominal. Se puede considerar como el nombre del estudiante (en realidad, sustituye al nombre). Tanto el ID, como el nombre de un estudiante, no suelen tener relación con las otras variables, por lo que más adelante veremos que no se contemplan en el análisis de los datos.
Tiene utilidad para cruzar los datos con otra tabla que tenga los nombres de los estudiantes, pero no para sacar conclusiones a partir de ella.
asignatura
# Muestra de 5 valores al azar de la variable asignatura
random_sample = df['asignatura'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
802 Matemáticas 354 Matemáticas 1 Matemáticas 1481 Matemáticas 1331 Matemáticas Name: asignatura, dtype: object
Al parecer, la variable asignatura solo toma un valor: ‘Matemáticas’. Sabemos que es así por como hemos definido el dataframe, pero como hemos dicho antes, los normal es que estos datos no los sepamos de antemano, y debamos comprobarlos.
Podemos pensar que nuestro dataframe es una versión filtrada de otro conjunto de datos más grande que tiene las notas de todas las asignaturas. Pero debemos comprobarlo:
# Calcular el número de valores únicos en la columna "asignatura"
num_asignaturas_unicas = df['asignatura'].nunique()
# Mostrar el resultado
print(f"El número de asignaturas únicas es: {num_asignaturas_unicas}")
El número de asignaturas únicas es: 1
Efectivamente, la variable solo toma un valor.
Esto la hace inútil en términos de análisis (no hay variabilidad en ella, pero ya llegaremos ahí).
Ahora nos limitaremos a clasificarla como variable estadística, diciendo que es, al igual que el ID, una variable cualitativa o categórica nominal.
De paso, surge otro tema: un lector atento podría decir que si el dataframe está filtrado y solo tiene las notas de matemáticas, es una muestra de todas las notas del año académico 2024-2025. Pero hemos dicho que nuestro dataframe contiene la población de las notas. ¿En qué quedamos?
Es importante entender que la población de estudio es la que se define en el experimento, y hemos definido la población como el conjunto de notas de matemáticas de los alumnos de segundo de bachillerato del instituto Luis Vives de Valencia, en el año académico 2024-2025.
Si, por ejemplo, hubiésemos definido a la población como el conjunto de notas de matemáticas de segundo de bachillerato de todos los institutos de España, en el año académico 2024-2025, nuestro dataframe sería una muestra, con los datos del instituto Luis Vives.
Pero zanjemos el tema: en este caso, tal y como se ha definido el experimento, el conjunto de notas de nuestro dataframe es la población.
tema
# Muestra de 5 valores al azar de la variable tema
random_sample = df['tema'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
1008 Tema 9 40 Tema 1 243 Tema 4 481 Tema 2 1393 Tema 4 Name: tema, dtype: object
Cuando le pedimos a Python que nos muestre valores elegidos al azar, vemos que la variable toma los valores «Tema n», siendo «n» el número del tema.
Recordemos que estamos simulando que no sabemos mucho del dataframe, así que intentaremos ver más detalles: todos los valores, ordenados alfabéticamente:
# Obtener valores únicos de la columna "tema" y ordenarlos alfabéticamente
temas_unicos = sorted(df['tema'].unique())
# Mostrar el resultado
print("Listado de temas por orden alfabético:")
for tema in temas_unicos:
print(tema)
Listado de temas por orden alfabético: Tema 1 Tema 10 Tema 2 Tema 3 Tema 4 Tema 5 Tema 6 Tema 7 Tema 8 Tema 9
Quitando el problema de que 10 está antes que el 2 (ahora no vamos a detenernos aquí), vemos que «n» va de 1 a 10.
Tema es, por tanto, una variable cualitativa o categórica ordinal, puesto que el Tema 1 va antes que el Tema 2, y así hasta 10.
fecha
# Muestra de 5 valores al azar de la variable fecha
random_sample = df['fecha'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
1260 2024-09-01 10 2024-09-01 676 2025-02-16 1263 2024-11-24 1063 2024-11-24 Name: fecha, dtype: datetime64[ns]
La fecha es una variable tipo DateTime para Python. Estas variables son muy traicioneras. Para empezar, hay que estar seguro del formato.
En este caso, una revisión aleatoria nos sirve para para ver que el formato es aaaa-mm-dd. Ya entraremos en detalles sobre este tipo de variable. Por ahora mi recomendación es, si se quiere saber más, consultar la documentación oficial de numpy (si se está trabajando en Python).
Desde un punto de vista estadístico, la fecha puede ser una variable cualitativa o categórica ordinal (al igual que «tema») o, dependiendo del contexto, también se puede considerar como una variable cuantitativa continua.
Si solo nos interesan las relaciones de orden entre fechas, y la variable se usa para ordenar eventos o situaciones, entonces la estamos tratando como una variable ordinal. Si, en cambio, las expresamos como un rango continuo de valores para realizar operaciones aritméticas, como la diferencia entre fechas, entonces es una variable cuantitativa continua. Nótese, sin embargo, que incluso siendo considerada como como cuantitativa, hay operaciones aritméticas que carecerían de sentido. Promediar el tiempo que se tarda en hacer algo, o la altura de un grupo de personas, o el número de crímenes por cada 1.000 habitantes es perfectamente lícito. Pero me cuesta encontrar un caso en el que promediar fechas propiamente dichas nos aporte información relevante… Otra cosa distinta es promediar las diferencias entre fechas. En ese caso, es posible encontrar aplicaciones prácticas. Por ejemplo, cuantos días, de media, pasan entre la primera vista a una tienda online, y la primera compra. Para obtener ese dato antes debemos calcular para cada caso en el que se ha producido una primera compra, la diferencia entre la fecha de esa primera compra y la primera visita a la tienda.
En el caso concreto que nos ocupa, en el que la fecha la estamos usando para ordenar cada examen en el tiempo, podemos considerarla como una variable cualitativa o categórica ordinal.
nota
# Muestra de 5 valores al azar de la variable nota
random_sample = df['nota'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
40 7.29 100 5.67 1276 6.12 887 5.09 1548 7.60 Name: nota, dtype: float64
Aquí tenemos un caso interesante. «Nota» es una variable numérica, y Python la ha tipificado como tal (float64). Si es float, es porque tiene decimales.
Como comentamos antes, se observa una clara tendencia a clasificar cualquier variable numérica con decimales como continua, aunque en realidad no lo sea. Vamos a explicar las razones de esto.
Conceptualmente, las notas SON continuas (como la estatura, el peso, el índice de masa corporal, la distancia, etc…).
Sin embargo, y si nos fijamos, las notas de nuestro dataframe están redondeadas a 2 decimales. Esto se hace porque, en la práctica, trabajar con más de 2 decimales en este caso es un poco exagerado.
Por lo tanto, tenemos huecos. Entre un 7.44 y un 7.45 no hay nada. No vamos a encontrar, por ejemplo, un 7.443, o un 7.4432.
Recordemos aquí la definición de una variable continua: «una variable continua puede asumir cualquier valor a lo largo de un intervalo de recta, incluyendo cualquier valor posible entre dos variables determinadas» (Johnson & Kuby).
Nuestra variable «nota» no cumple esa condición. Esto significa que la variable se ha «discretizado», y «nota», en este caso, es una variable cuantitativa o numérica discreta. Puede tomar muchos valores, es cierto, pero son finitos.
Ahora bien, la cosa no acaba aquí. Aunque efectivamente «nota» es una variable numérica discreta en este caso, en muchos aspectos se suele tratar como si fuera continua.
Por ejemplo, cuando hemos graficado la distribución de notas en el apartado de distribución de datos, lo hemos hecho con un gráfico de densidad, que no tiene escalones, como si entre el 7.44 y 7.45 hubiera valores. Con las variables discretas, las distribuciones se grafican con histogramas, tal y como hemos visto antes:
# Definir los bordes de los bins
bins = np.linspace(0, 10, 21) # 21 porque queremos 20 intervalos
# Imprimir los bordes de los bins
print("Bordes de los bins:", bins)
# Graficar el histograma de las notas usando Seaborn
plt.figure(figsize=(10, 6))
sns.histplot(data=df['nota'], bins=bins, kde=False, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.show()
Bordes de los bins: [ 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. 7.5 8. 8.5 9. 9.5 10. ]
En el histograma superior se han creado 20 contenedores (bins), en los que se han agrupado varias notas en cada contenedor. En cada uno, están las notas en saltos de 0.50, por lo que el primer contenedor va de [1.50 a 2.00), el segundo de [2.00 a 2.49), etc… Es decir, en el segundo contenedor, por ejemplo, tendremos notas como 2.01, 2.23, 2.45, etc… Los corchetes cuadrados indican que el valor está en el intervalo, y el redondo que no.
Si aumentamos el número de contenedores (por ejemplo en saltos pequeñitos de 0.1), los contenedores son más estrechos.
En este caso, si la nota mínima es 1.5, el primer contenedor contendrá las notas del intervalo [1.50, 1.60), pasando por 1.51, 1.52, 1.53… hasta 1.59. Recordemos que no hay notas inferiores a 3, por lo que al forzar lo bordes de 0 a 10 los gráficos se ven desplazados hacia la derecha.
# Definir los bordes de los bins del tamaño de 0.1
bins = np.arange(0, 10.1, 0.1)
# Graficar el histograma de las notas usando Seaborn
plt.figure(figsize=(10, 6))
sns.histplot(data=df['nota'], bins=bins, kde=False, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.show()
Si aumentamos más aún el número de contenedores, por ejemplo, en saltos de 0.01, tenemos un histograma que nos muestra todas las notas, desde el 0.00 al 10.00, pasando por 0.01, 4.52, 7.44, 8.78, 9.45… por poner sólo algunos ejemplos.
# Definir los bordes de los bins del tamaño de 0.01
bins = np.arange(0, 10.1, 0.01)
# Graficar el histograma de las notas usando Seaborn
plt.figure(figsize=(10, 6))
sns.histplot(data=df['nota'], bins=bins, kde=False, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.show()
Elegir el número correcto de contenedores en un histograma, con el fin de visualizar adecuadamente la verdadera naturaleza de una distribución, es un arte. Sobre todo si la variable, aunque discreta, tiene decimales.
Con un gráfico de densidad, en lugar de un histograma de frecuencias, no hace falta preocuparse tanto por eso.
Fijaros lo que pasa si, sobre los histogramas anteriores, pintamos la curva de densidad. A vuestro juicio, ¿qué histograma se parece más a dicha curva?
# Definir los bordes de los bins del tamaño de 0.1
bins = np.linspace(0, 10, 21) # 21 porque queremos 20 intervalos
# Graficar el histograma de las notas usando Seaborn
plt.figure(figsize=(10, 6))
sns.histplot(data=df['nota'], bins=bins, kde=True, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.show()
# Definir los bordes de los bins del tamaño de 0.1
bins = np.arange(0, 10.1, 0.1)
# Graficar el histograma de las notas usando Seaborn con la curva de densidad
plt.figure(figsize=(10, 6))
sns.histplot(data=df['nota'], bins=bins, kde=True, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.show()
# Definir los bordes de los bins del tamaño de 0.1
bins = np.arange(0, 10.1, 0.01)
# Graficar el histograma de las notas usando Seaborn
plt.figure(figsize=(10, 6))
sns.histplot(data=df['nota'], bins=bins, kde=True, color='blue')
plt.title('Distribución de Notas de la Población')
plt.xlabel('Nota')
plt.ylabel('Frecuencia')
plt.show()
Aunque es importante saber que un gráfico de densidad no es lo mismo que un histograma de frecuencias (de nuevo nos hemos estado adelantando un poco), ambos nos están mostrando la «forma» de la distribución. En este caso, las notas se distribuyen en torno a un valor central, 6.5, y son menos frecuentes en los extremos.
Es por eso que, cuando hay decimales, a nivel de tratamiento gráfico se suele optar por tratar la variable como continua, aunque sea discreta.
Probabilidades
Otra razón por la que hay variables discretas que se tratan como continuas tiene que ver con algo a lo que aún no hemos llegado: las probabilidades de obtener una nota concreta.
Supongamos que el responsable de orientación escolar les pide ahora a los alumnos que han hecho el experimento que calculen la probabilidad de que un alumno cualquiera tenga un 8.00 en matemáticas.
Los alumnos se dan cuenta entonces que mientras más notas posibles se puedan registrar, menor es la probabilidad de tener una nota concreta.
De hecho, ellos ya lo intuían de manera natural. Cuando entre colegas apostaban por la nota que iban a sacar en el siguiente examen, no decían «un 8.45». Solían decir algo así como «más de un 8». Eso es un intervalo que va de 8.01 a 10.00, que es mucho más probable que sacar exactamente 8.45, cuya probabilidad es cercana a 0.
Cuando hay decimales, aunque haya saltos entre los valores y la variable se haya «discretizado», acertar el valor exacto es muy, muy difícil, casi imposible. Ya llegaremos. Ahora diremos que cuando eso pasa, a efectos de cálculos de ciertas cosas, la variable, aunque discreta, se trata como continua.
Todo esto explica la confusión natural que nos lleva a decir, sin pensar mucho, que si hay decimales la variable es continua.
Si queremos aprobar el examen de estadística, debemos decir que la variable «nota», en este caso, es discreta. Si queremos analizarla, es conveniente tratarla como continua. Nadie dijo que esto fuera fácil.
calificacion
La calificación en este dataframe, es una representación con palabras de las notas obtenidas.
# Obtener valores únicos de la columna "calificacion" y ordenarlos alfabéticamente
calificacion_unicos = sorted(df['calificacion'].unique())
# Mostrar el resultado
print("Listado de calificaciones por orden alfabético:")
for calificacion in calificacion_unicos:
print(calificacion)
Listado de calificaciones por orden alfabético: aprobado notable sobresaliente suspenso
A estas alturas debería estar claro «calificación» es una variable cualitativa o categórica ordinal, por lo que su orden natural, de menor a mayor nota, sería suspenso, aprobado, notable y sobresaliente.
estatura
# Muestra de 5 valores al azar de la variable estatura
random_sample = df['estatura'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
1497 164.220792 1043 184.949382 280 163.768595 705 164.867864 371 181.870303 Name: estatura, dtype: float64
Parece que en el instituto Luis Vives de Valencia se toman muy en serio esto de medir a los estudiantes de forma precisa. Tenemos valores que parecen ser centímetros con hasta seis posiciones decimales. Deben de tener en el laboratorio un metro láser de la NASA, que registra la estatura con mucho detalle.
En este caso, hablar de variable numérica continua tiene todo el sentido del mundo. Aún cuando la discretizáramos quitando todos los decimales, y quedándonos con la parte entera redondeada al decimal más cercano, tratarla como contínua sería lo más lógico. En ese caso, todo lo dicho para la variable «nota» aplicaría aquí.
sexo
# Muestra de 5 valores al azar de la variable sexo
random_sample = df['sexo'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
93 M 38 H 769 H 1447 M 1547 H Name: sexo, dtype: object
Sexo es una variable categórica nominal. Según qué casos, puede ser dicotómica o no. Si toma sólo dos valores, es dicotómica. Si toma más de dos, no lo es.
# Calcular el número de valores únicos en la columna "asignatura"
num_asignaturas_unicas = df['sexo'].nunique()
# Mostrar el resultado
print(f"El número de valores únicos de la variable sexo es: {num_asignaturas_unicas}")
El número de valores únicos de la variable sexo es: 2
En este caso, la variable es dicotómica. Podría pasar que no lo fuera, y que el dataframe tuviera valores como no-binario, no-especificado, etc…
Saber este tipo de cosas es importante, porque en fases posteriores esto nos permitirá decidir cómo tratar la variable si necesitamos convertirla en numérica, para su tratamiento y modelización.
Una variable dicotómica se puede transformar en ceros y unos sin alterar el número de columnas del dataframe. Si no es dicotómica, se deben usar otras alternativas para transformarla en numérica. Ya las veremos.
tiempo_estudio
# Muestra de 5 valores al azar de la variable tiempo_estudio
random_sample = df['tiempo_estudio'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
312 194 291 299 782 179 1425 282 804 179 Name: tiempo_estudio, dtype: int64
Esto es interesante. Si no hubiésemos generado nosotros el dataframe con datos de ejemplo, especificando que los valores de tiempo de estudio estuvieran en minutos, con sólo ver estos datos no podríamos estar seguros.
¿Qué estamos viendo? ¿Horas, minutos, segundos, flerps?
Muchas veces nos encontraremos este tipo de problemas, y lo mejor es acudir a la fuente, y asegurarse de la unidad de medida.
En cualquier caso, es una variable numérica. ¿Sabría decir el lector si es discreta o contínua? Y si es discreta ¿tiene sentido tratarla como contínua?
grupo
# Muestra de 5 valores al azar de la variable grupo
random_sample = df['grupo'].sample(5)
# Mostrar los valores seleccionados al azar
print(random_sample)
199 C 1418 C 242 C 55 C 1538 B Name: grupo, dtype: object
# Obtener valores únicos de la columna "calificacion" y ordenarlos alfabéticamente
grupos_unicos = sorted(df['grupo'].unique())
# Mostrar el resultado
print("Listado de grupos por orden alfabético:")
for grupo in grupos_unicos:
print(grupo)
Listado de grupos por orden alfabético: A B C D
En el caso de los grupos, tenemos cuatro valores posibles: A, B, C, D. Estos valores se pueden ordenar alfabéticamente, y la A está antes que la B, la B antes que la C, y la C antes de la D.
Aún sabiendo esto, ¿podríamos decir que la variable «grupo» es ordinal?
Las calificaciones lo son, sin duda. Los años también. Las posiciones de una carrera (primero, segundo, tercero…).
Si volvemos al ejemplo de las calificaciones, podríamos cambiar Sobresaliente por A, Excelente por B, Muy bien por C, Bien por D, y Suspenso por E. En ese caso, el orden alfabético coincide con el orden intrínseco de la variable.
Pero podríamos haber nombrado los grupos por colores: A es Azul, B es Blanco, C es Caoba y D es Dorado.
Si los ordenamos alfabéticamente, Azul iría antes que Blanco, Blanco antes que Caoba. Y así hasta el Dorado.
¿Tiene sentido decir que Azul va primero que Blanco. ¿O que Dorado va después de Caoba?
En este caso, los grupos son nombres de un conjunto de alumnos, y no tienen orden intrínseco. «Grupo», por tanto, sería una variable cualitativa o categórica nominal.
aprobado
Hemos llegado a la última variable de nuestro dataframe de ejemplo. Ya la habíamos tratado antes cuando, al principio de este apartado, pusimos el ejemplo de una variable que Python (y R) tipifican como numéricas cuando son, en esencia, nominales dicotómicas.
Consideraciones finales
En este artículo hemos intentado sentar las bases, desde el verdadero principio, de una disciplina realmente excitante, como es la Ciencia de Datos.
No es casualidad que hayamos empezado por conceptos estadísticos. La estadística, y la probabilidad, son las madres de lo que ahora tenemos en materia de Inteligencia Artificial, desde las regresiones, hasta las Inteligencia Artificial Generativa, pasando por los algoritmos de Machine Learning tradicionales.
De hecho, y simplificando mucho, ChatGPT y Gemini generan textos en función de la probabilidad de que una palabra siga a otra. Para poder hacer eso, calculan matrices de vectores… Otra vez nos estamos dejando llevar por la emoción. Vayamos por partes.
Nuestra intención es desarrollar una serie de artículos secuenciales que vayan desgranando, paso a paso, los fundamentos de una disciplina que, en cierta medida, está cambiando el mundo.
En este viaje, veremos conceptos de probabilidad, álgebra (sobre todo matricial) y algo de cálculo, pero el objetivo final no es dar una clase magistral sobre estas materias, si no explicar qué papel juegan en el contexto que nos ocupa.
Llegados aquí, no queda más que agradecer al lector su paciencia, y felicitarlo por sus ansias de aprender.
Bibliografía y referencias
- Johnson, R. & Kuby, P. (2008). Estadistica elemental: lo esencial (10a ed.). Cengage Learning Editores S.A.
- Freedman, D., Pisani, R., & Purves, R. (2007). Statistics (4a ed.). WW Norton.
Artículo siguiente: Tablas de frecuencia y gráficos de distribución —>